最近好好整理了一下有关RSA的知识点,以及其在CTF比赛中的应用

基础知识

数论知识

在这边简单阐述rsa需要用到的数论知识：

互质关系，两个正整数除了1以外没有其他公因子，就称这两个数为互质关系（coprime）
欧拉函数:任意给定正整数n，计算小于等于n正整数中，与n构成互质关系的个数
欧拉定理:

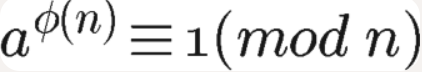
也就是说，a的φ(n)次方被n除的余数为1。或者说，a的φ(n)次方减去1，可以被n整除。比如，3和7互质，而7的欧拉函数φ(7)等于6，所以3的6次方（729）减去1，可以被7整除（728/7=104）。

关于欧拉函数的结论很多，可以去别的地方查找，但是这边只介绍两个

（1）如果n是质数，则 φ(n)=n-1

（2）如果n可以分解成两个互质的整数之积：

n = p1 * p2 ==> φ(n) = φ(p1p2) = φ(p1)φ(p2)

模反元素：如果两个正整数a和n互质，那么一定可以找到整数b，使得ab-1被n整除

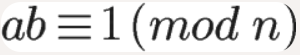
比如，3和11互质，那么3的模反元素就是4，因为 (3 × 4)-1 可以被11整除。显然，模反元素不止一个， 4加减11的整数倍都是3的模反元素 {…,-18,-7,4,15,26,…}，即如果b是a的模反元素，则 b+kn 都是a的模反元素。
欧拉定理可以用来证明模范元素必然存在

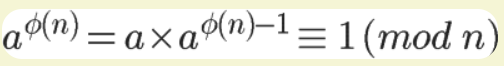
rsa加密算法

随机选择两个不相等的质数p和q
计算p和q的乘积n

n = p * q

计算n的欧拉函数φ(n)

1
2
3

φ(n) =  (p-1) (q-1) 

推算：φ(n) =  φ(p*q) = φ(p1)φ(p2) = (p-1) (q-1)

随机选择一个整数e，条件：（1<e<φ(n)）,且e和φ(n)互质
计算e对于φ(n)的模反元素d

ed ≡ 1 (mod φ(n))

ed - 1 = kφ(n)

ex + φ(n)y = 1，也就是求左边二元一次方程的解

将n和e扩展成公钥（n，e），n和d封装成私钥（n，d）

1
2
3

假设n = 3233，e = 17，d = 2753

公钥：（3233，17）	私钥（3233，2753）

rsa算法的可靠性

一共出现了6个数字：p/q/φ(n)/e/d，公钥用到了两个，其余四个整数都是不公开的，其中最关键的是d，一旦d泄，就等于私钥泄露

结论：如果n可以被因数分解，d就可以被算出，也就意味这私钥被破解。除了暴力破解，还没有发现别的有效方法，目前被破解的最长RSA密钥就是768位。
加密与解密

（1）加密需要公钥（n,e），假设m就是要加密的值，比如ascii码值或者Unicode值(m必须为整数，且小于n)，那么加密后的值为c
1
m ** e ≡ c (mod n)
爱丽丝的例子，爱丽丝的公钥为(3233,17)

假设鲍勃要加密的值是65，通过下面的计算，2790就是鲍勃发送的值
1
65 ** 17 ≡ 2790 (mod 3233)
（2）解密需要私钥（n,d），下面的等式一定成立
1
c ** d ≡ m (mod n)
还是爱丽丝的例子，爱丽丝就用自己的私钥(3233,2735)进行解密
1
2790 ** 2753 ≡ 65 (mod 3233)
因此，爱丽丝就知道鲍勃加密前的密文就是65

当然还有关于上述公示的证明，可以参考阮老师的博客：

http://www.ruanyifeng.com/blog/2013/06/rsa_algorithm_part_one.html

http://www.ruanyifeng.com/blog/2013/07/rsa_algorithm_part_two.html

yafu的使用

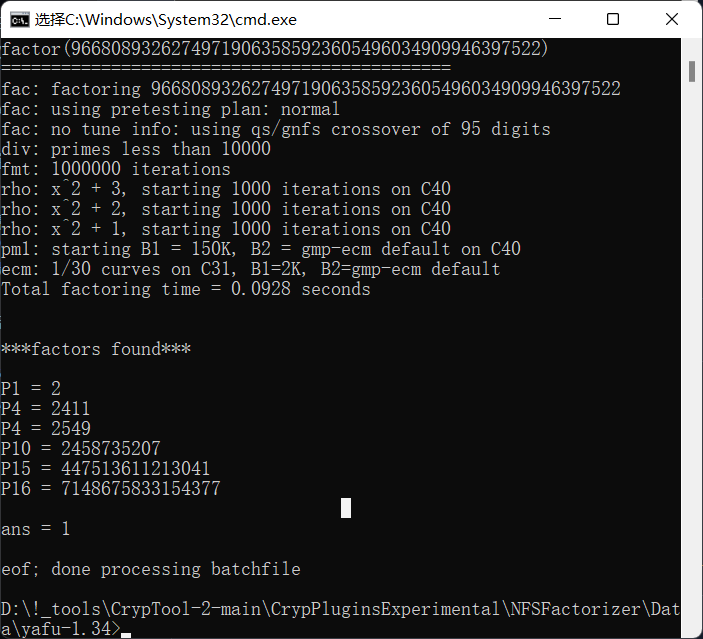
最常用的方法是在命令行中直接使用factor()函数分解

1	yafu-x64 factor(n)

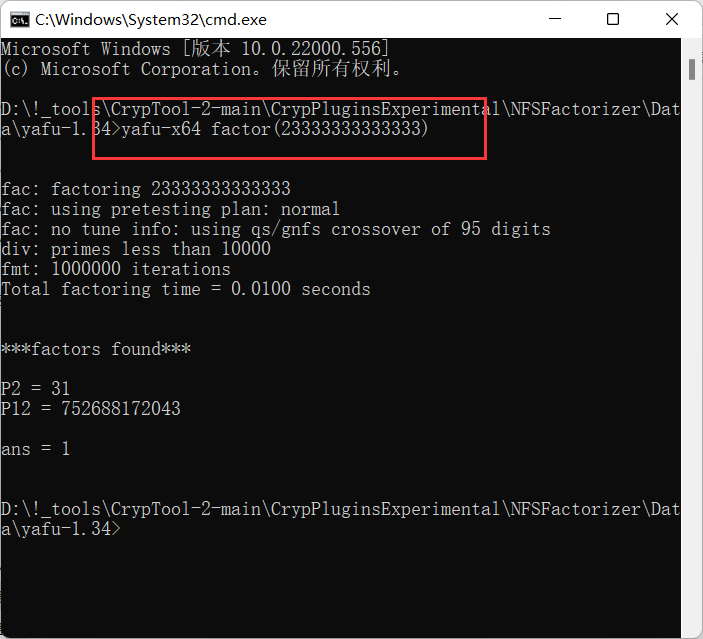
当然，命令行可能不支持太长的n

新建一个pcat.txt，注意最后一定得换行，运行命令

1	yafu-x64 “factor(@)” -batchfile pcat.txt

中国剩余定理

资料参考

我来举个简单的例子来理解一下CRT的代码实现。

import gmpy2

#ai是余数，mi是除数，且除数mi互质
a1,m1 = 1,3 # x % 3 == 1 
a2,m2 = 3,5 # x % 5 == 3 
a3,m3 = 2,7 # x % 7 == 2 

# M为除数的乘积，即M = ∏ mi
M = m1 * m2 * m3

# Mi是除了自身的除数的乘积
M1 = M // m1 # M1 = 35
M2 = M // m2 # M2 = 21
M3 = M // m3 # M3 = 15

# ti就是Mi关于mi的模逆
t1 = gmpy2.invert(M1,m1) # t1 = 2  35*2 % 3 == 1
t2 = gmpy2.invert(M2,m2) # t2 = 1
t3 = gmpy2.invert(M3,m3) # t3 = 1

# x是ai*ti*Mi项的和
x = a1 * t1 * M1 + a2 * t2 * M2 + a3 * t3 * M3
s = x%M
print(s) # 163 % 105 = 58

结果不唯一，x + kM都可以是结果

所以如果是求最小值，可以x%M

上面的代码简化一下，就可以变成下面的代码：

import gmpy2

def CRT(aList, mList):
    M = 1
    for i in mList:
        M = M * i   #计算M = ∏ mi
    x = 0
    for i in range(len(mList)):
        Mi = M // mList[i]   #计算Mi
        ti = gmpy2.invert(Mi, mList[i]) #计算Mi的逆元
        x += aList[i] * Mi * ti #构造x各项
    x = x % M
    return x

aList = [1,3,2]
mList = [3,5,7]
print(CRT(aList,mList))

例题：蓝桥杯2022年python B组试题B：寻找整数

import gmpy2

def CRT(aList, mList):
    M = 1
    for i in mList:
        M = M * i   #计算M = ∏ mi
    #print(M)
    x = 0
    for i in range(len(mList)):
        Mi = M // mList[i]   #计算Mi
        Mi_inverse = gmpy2.invert(Mi, mList[i]) #计算Mi的逆元
        x += aList[i] * Mi * Mi_inverse #构造x各项
    x = x % M
    return x


nList = [2,3,5,7,11,13,17,19,23,29,31,37,41,43,47]
cList = [1,2,4,4,0, 10,0, 18,15,16,27,22,1, 11,5]
print(CRT(cList,nList))
# 2022040920220409

各种题型

基础解法

rsarsa （基础解法）

Math is cool! Use the RSA algorithm to decode the secret message, c, p, q, and e are parameters for the RSA algorithm.


p =  9648423029010515676590551740010426534945737639235739800643989352039852507298491399561035009163427050370107570733633350911691280297777160200625281665378483
q =  11874843837980297032092405848653656852760910154543380907650040190704283358909208578251063047732443992230647903887510065547947313543299303261986053486569407
e =  65537
c =  83208298995174604174773590298203639360540024871256126892889661345742403314929861939100492666605647316646576486526217457006376842280869728581726746401583705899941768214138742259689334840735633553053887641847651173776251820293087212885670180367406807406765923638973161375817392737747832762751690104423869019034

Use RSA to find the secret message

import gmpy2
p = 9648423029010515676590551740010426534945737639235739800643989352039852507298491399561035009163427050370107570733633350911691280297777160200625281665378483
q = 11874843837980297032092405848653656852760910154543380907650040190704283358909208578251063047732443992230647903887510065547947313543299303261986053486569407
e = 65537
c = 83208298995174604174773590298203639360540024871256126892889661345742403314929861939100492666605647316646576486526217457006376842280869728581726746401583705899941768214138742259689334840735633553053887641847651173776251820293087212885670180367406807406765923638973161375817392737747832762751690104423869019034
n = p * q
d = gmpy2.invert(e, (q-1)*(p-1))
m = pow(c,d,n)
print(m)

首先我们需要求出d，这样就使得rsa私钥被泄露

介绍一个函数gmpy2.invert()函数，专门用来求模反的函数，需要求出的d就是e关于φ(n)的模反

n = p1 * p2 ==> φ(n) = φ(pq) = φ(p)φ(q) = (p - 1)(q - 1)

ed ≡ 1 (mod φ(n))

求出flag，也就是密文，c是明文（被加密之后的），需要求出求得d之后，计算

1	c ** d ≡ m (mod n)

转换成代码，m = pow(c,d,n)

RSAROOL (在线分解)

题目给出公钥{n,e}，因式分解求p和q

1 2	p = 18443 q = 49891

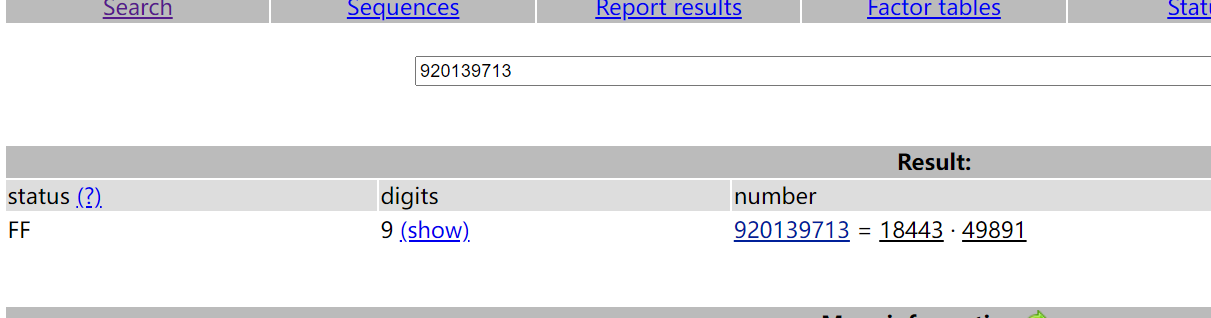
当然，因式分解python代码爆破也行：

import time
# 对一个数进行因式分解
def factorization(num):
    factor = []
    while num > 1:
        for i in range(num - 1):
            k = i + 2
            if num % k == 0:
                factor.append(k)
                num = int(num / k)
                break
    return factor


st = time.perf_counter()
print(factorization(920139713))
et = time.perf_counter()
print("用时:", et - st)

# [18443, 49891]

完整代码：

import gmpy2
n = 920139713
e = 19
p = 18443
q = 49891

# 读取数据，需要修改一下文本文档中的值
# lis = []
# with open("data.txt","r") as f:
# 	lines = f.readlines()
# 	for line in lines:
# 		lis.append(int(line.strip()))

lis = [704796792, 752211152, 274704164, 18414022, 368270835, 483295235, 263072905, 459788476, 483295235, 459788476, 663551792, 475206804, 459788476, 428313374, 475206804, 459788476, 425392137, 704796792, 458265677, 341524652, 483295235, 534149509, 425392137, 428313374, 425392137, 341524652, 458265677, 263072905, 483295235, 828509797, 341524652, 425392137, 475206804, 428313374, 483295235, 475206804, 459788476, 306220148]

flag = []
for i in lis:
	d = gmpy2.invert(e,(p-1)*(q-1))
	flag.append(chr(int(pow(i,d,n)))) # pow计算完成之后需要转成int

print("".join(flag))
# flag{13212je2ue28fy71w8u87y31r78eu1e2}

RSA (基础解法)

1 2	在一次RSA密钥对生成中，假设p=473398607161，q=4511491，e=17 求解出d作为flag提交

import gmpy2
p=473398607161
q=4511491
e=17
d = gmpy2.invert(e,(p-1)*(q-1))
print(d)
# flag{125631357777427553}

[ACTF新生赛2020]crypto-rsa0 (zip伪加密)

misc zip伪加密

参考链接：

zip格式共有三个数据区：压缩源文件数据区/压缩源文件目录区/压缩源文件目录结束标志

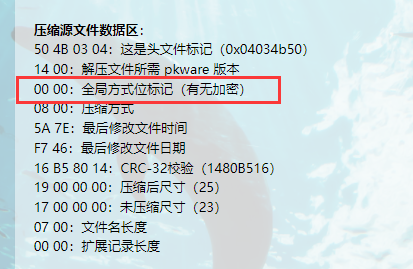
第一区的第三个字节和第二区的第四个字节都显示是否加密的信息.修改两个区域的加密信息，数字是奇数时为加密，数字为偶数时，则不加密。我们修改09 00 改成08 00

winhex打开查看

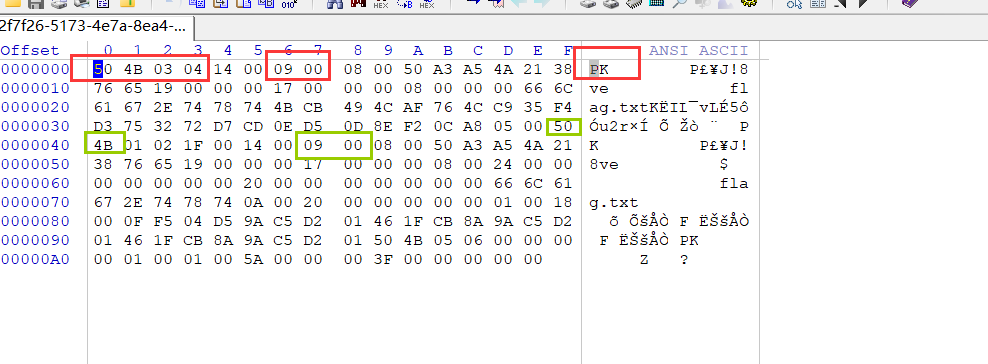
修改后：

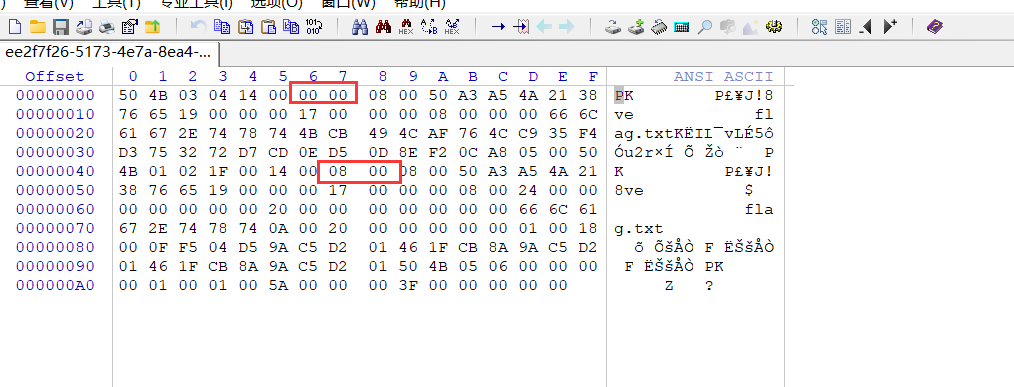
在来看这道题，放在winhex中打开，修改一下

1
2
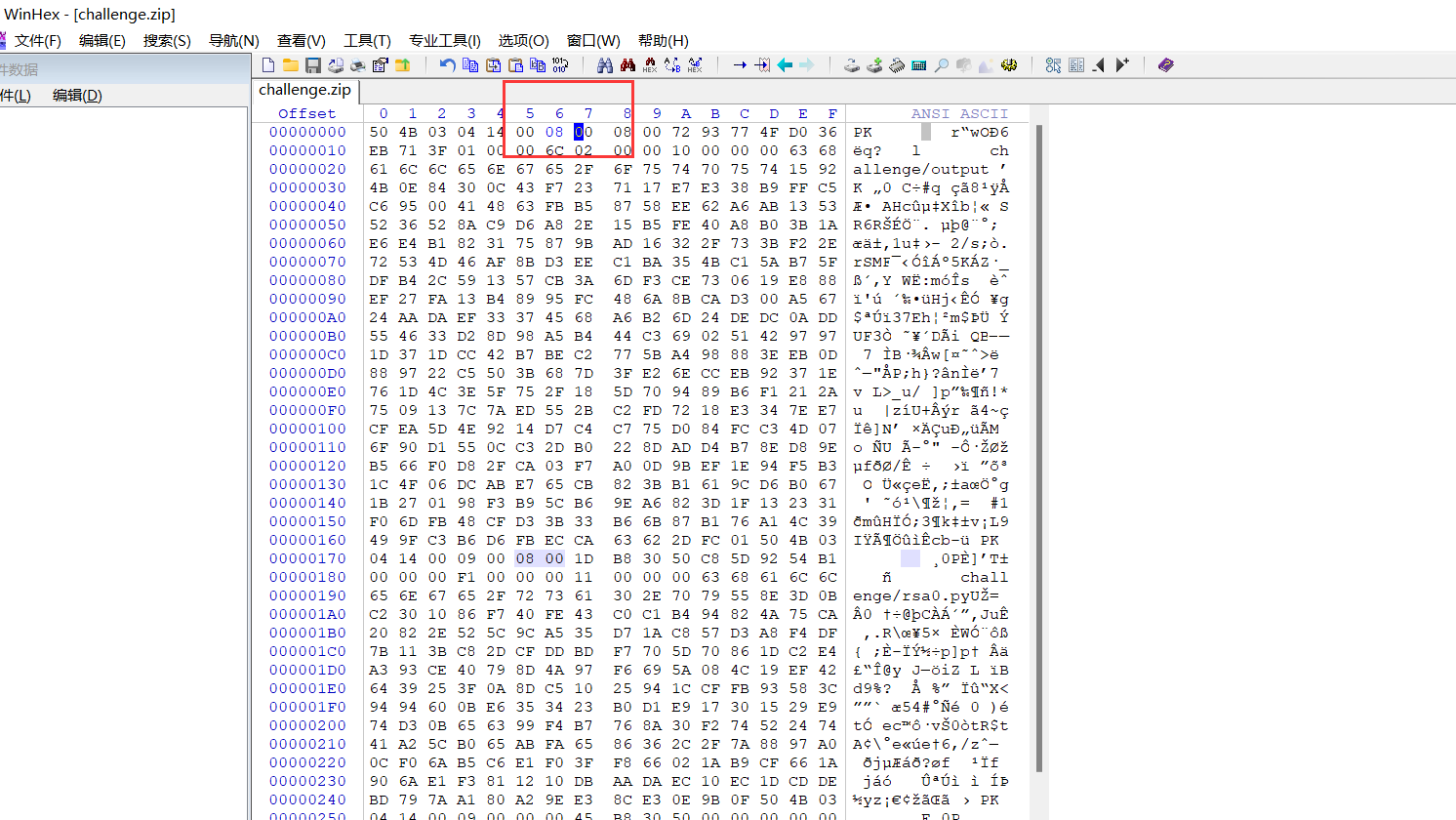
3

9018588066434206377240277162476739271386240173088676526295315163990968347022922841299128274551482926490908399237153883494964743436193853978459947060210411
7547005673877738257835729760037765213340036696350766324229143613179932145122130685778504062410137043635958208805698698169847293520149572605026492751740223
50996206925961019415256003394743594106061473865032792073035954925875056079762626648452348856255575840166640519334862690063949316515750256545937498213476286637455803452890781264446030732369871044870359838568618176586206041055000297981733272816089806014400846392307742065559331874972274844992047849472203390350

给了上述的三串数字，猜测是p/q/n，上代码：

from Crypto.Util import number
import gmpy2
p = 9018588066434206377240277162476739271386240173088676526295315163990968347022922841299128274551482926490908399237153883494964743436193853978459947060210411
q = 7547005673877738257835729760037765213340036696350766324229143613179932145122130685778504062410137043635958208805698698169847293520149572605026492751740223
c = 50996206925961019415256003394743594106061473865032792073035954925875056079762626648452348856255575840166640519334862690063949316515750256545937498213476286637455803452890781264446030732369871044870359838568618176586206041055000297981733272816089806014400846392307742065559331874972274844992047849472203390350
e = 65537
n = p*q
d = gmpy2.invert(e,(p-1)*(q-1))
m = pow(c,d,n)
print(number.long_to_bytes(m))

[GUET-CTF2019]BabyRSA （z3）

题目给出了(p+1)(q+1)，我们用z3来解就行

上代码：

from z3 import *
import gmpy2
from Crypto.Util.number import *

e = 0xe6b1bee47bd63f615c7d0a43c529d219
d = 0x2dde7fbaed477f6d62838d55b0d0964868cf6efb2c282a5f13e6008ce7317a24cb57aec49ef0d738919f47cdcd9677cd52ac2293ec5938aa198f962678b5cd0da344453f521a69b2ac03647cdd8339f4e38cec452d54e60698833d67f9315c02ddaa4c79ebaa902c605d7bda32ce970541b2d9a17d62b52df813b2fb0c5ab1a5
c = 0x50ae00623211ba6089ddfae21e204ab616f6c9d294e913550af3d66e85d0c0693ed53ed55c46d8cca1d7c2ad44839030df26b70f22a8567171a759b76fe5f07b3c5a6ec89117ed0a36c0950956b9cde880c575737f779143f921d745ac3bb0e379c05d9a3cc6bf0bea8aa91e4d5e752c7eb46b2e023edbc07d24a7c460a34a9a

p,q  = Ints('p q')
s = Solver()
s.add(p + q == 0x1232fecb92adead91613e7d9ae5e36fe6bb765317d6ed38ad890b4073539a6231a6620584cea5730b5af83a3e80cf30141282c97be4400e33307573af6b25e2ea)
s.add((p+1)*(q+1) == 0x5248becef1d925d45705a7302700d6a0ffe5877fddf9451a9c1181c4d82365806085fd86fbaab08b6fc66a967b2566d743c626547203b34ea3fdb1bc06dd3bb765fd8b919e3bd2cb15bc175c9498f9d9a0e216c2dde64d81255fa4c05a1ee619fc1fc505285a239e7bc655ec6605d9693078b800ee80931a7a0c84f33c851740)
print(s.check())
print(s.model())
q = 7021910101974335245794950722131367118195509913680915814438898999848788125908122655583911434165700354149914056221915541094395668546921268189522005629523759
p = 8228801334907462855397256098699556584084854642543205682719705217859576250443629616812386484797164506834582095674143447181804355696220642775619711451990971
n = p*q
d = gmpy2.invert(e,(p-1)*(q-1))
m = pow(c,d,n)
print(long_to_bytes(m))
# flag{cc7490e-78ab-11e9-b422-8ba97e5da1fd}

[HDCTF2019]bbbbbbrsa (爆破e)

题目给出了n和q，base64解码一下c，e的范围不是很大，所以直接暴力循环e就可以

import base64
from Crypto.Util.number import *
import gmpy2

n = 37421829509887796274897162249367329400988647145613325367337968063341372726061
p = 177077389675257695042507998165006460849
q = n // p
c = bytes("==gMzYDNzIjMxUTNyIzNzIjMyYTM4MDM0gTMwEjNzgTM2UTN4cjNwIjN2QzM5ADMwIDNyMTO4UzM2cTM5kDN2MTOyUTO5YDM0czM3MjM"[::-1],"utf-8")
c = int(str(base64.b64decode(c),"utf-8"))
print(c)

phi = (p-1) * (q-1)
for e in range(50000,70000):
	if gmpy2.gcd(e,phi) != 1:
		continue
	d = gmpy2.invert(e,phi)
	m = pow(c,d,n)
	flag = str(long_to_bytes(m))
	print(e,flag)
	if "flag" in flag or "CTF" in flag or "ctf" in flag:
		break
 #flag{rs4_1s_s1mpl3!#}

RSA (公钥解析1)

题目给出了一个key后缀文件和一个enc后缀的文件

需要进行公钥解析：

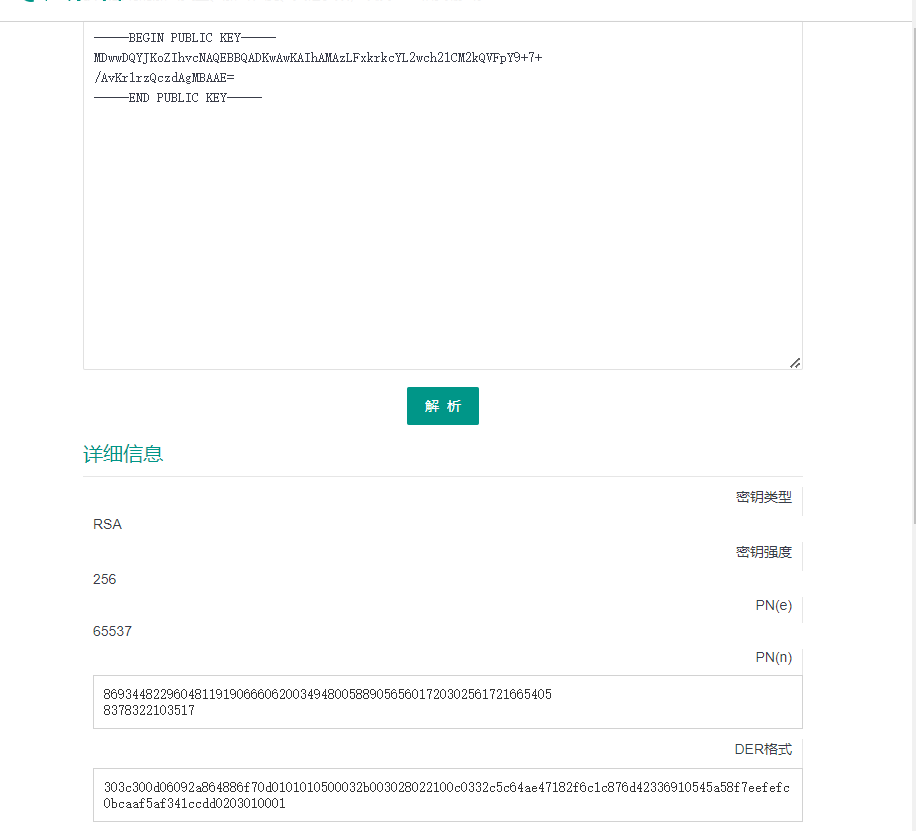
上代码：

from Crypto.Util import number
import gmpy2
n = 86934482296048119190666062003494800588905656017203025617216654058378322103517
e = 65537
p = 285960468890451637935629440372639283459
q = 304008741604601924494328155975272418463

# with open("flag.enc","rb") as f:
# 	s = f.read().strip()
# 	print(number.bytes_to_long(s))

c = 29666689760194689065394649908301285751747553295673979512822807815563732622178

d = gmpy2.invert(e,(q-1)*(p-1))

m = gmpy2.powmod(c,d,n)
print(number.long_to_bytes(m))

[AFCTF2018]可怜的RSA (公钥解析2 + PKCS1_OAEP)

我们也可以使用Crypto.PublicKey.RSA包中的函数来导入给出的public.key文件

import base64
from Crypto.Util.number import *
import gmpy2
from Crypto.PublicKey import RSA

with open("public.key","r") as f:
	pub = RSA.importKey(f.read())
	n = pub.n
	e = pub.e 
print(n,"\n",e)
# n = 79832181757332818552764610761349592984614744432279135328398999801627880283610900361281249973175805069916210179560506497075132524902086881120372213626641879468491936860976686933630869673826972619938321951599146744807653301076026577949579618331502776303983485566046485431039541708467141408260220098592761245010678592347501894176269580510459729633673468068467144199744563731826362102608811033400887813754780282628099443490170016087838606998017490456601315802448567772411623826281747245660954245413781519794295336197555688543537992197142258053220453757666537840276416475602759374950715283890232230741542737319569819793988431443 
# e = 65537

分解n,当然可以使用在线网站

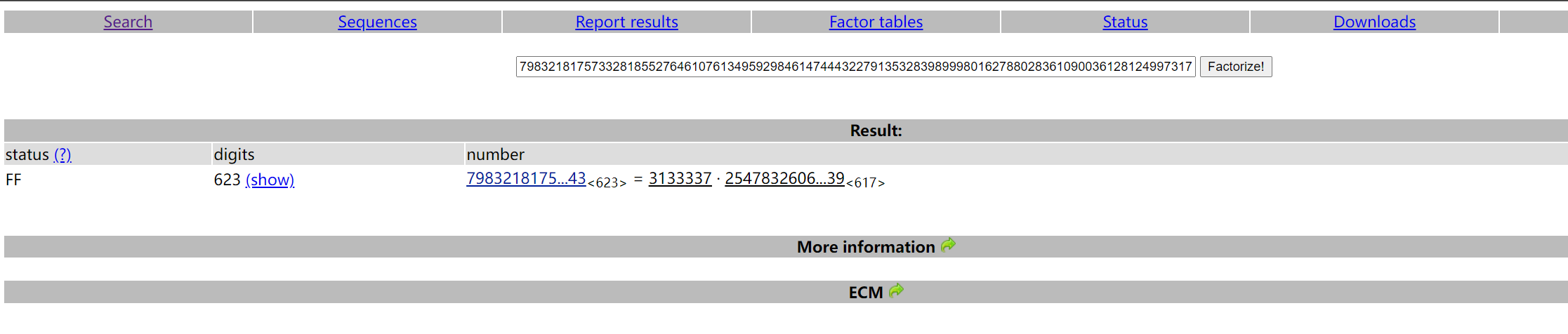
然后是从flag.ence中读取c，一开始我使用的是平常的m = pow(c,d,n)，会出错。

–正解–

打包密钥之后，使用PKCS1_OAEP填充模式来解

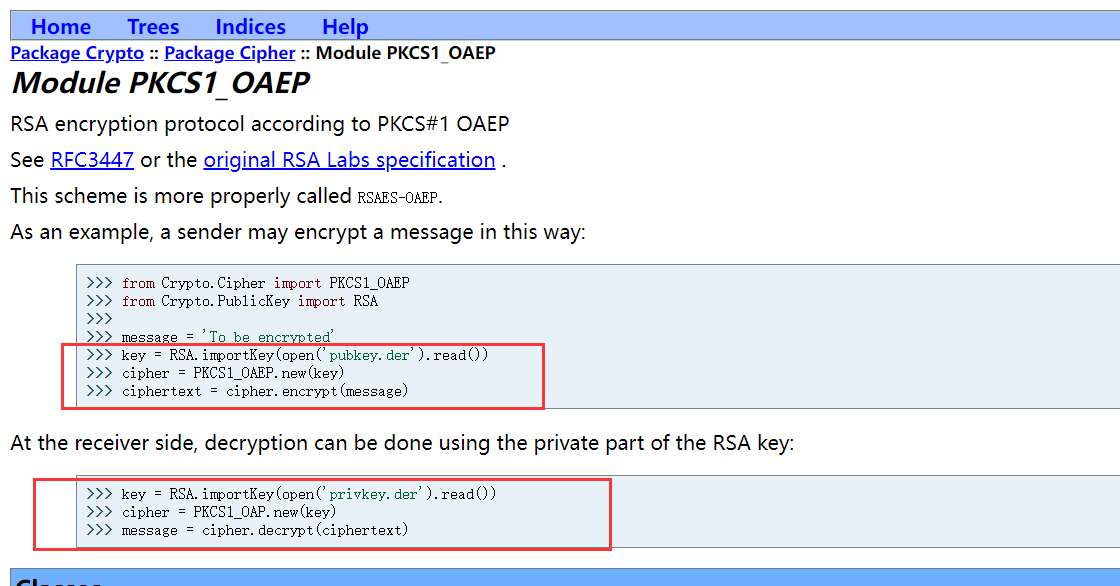
from base64 import *
from Crypto.Cipher import PKCS1_OAEP
from Crypto.Util.number import *
import gmpy2
from Crypto.PublicKey import RSA

with open("public.key","r") as f:
	pub = RSA.importKey(f.read())
	n = pub.n
	e = pub.e 

q = 25478326064937419292200172136399497719081842914528228316455906211693118321971399936004729134841162974144246271486439695786036588117424611881955950996219646807378822278285638261582099108339438949573034101215141156156408742843820048066830863814362379885720395082318462850002901605689761876319151147352730090957556940842144299887394678743607766937828094478336401159449035878306853716216548374273462386508307367713112073004011383418967894930554067582453248981022011922883374442736848045920676341361871231787163441467533076890081721882179369168787287724769642665399992556052144845878600126283968890273067575342061776244939
p = 3133337
d = int(gmpy2.invert(e,(p-1)*(q-1)))

key_info = RSA.construct((n, e, d, p, q))
key = RSA.importKey(key_info.exportKey())
key = PKCS1_OAEP.new(key)
with open('flag.enc', 'r') as f:
	c = b64decode(f.read())

flag = key.decrypt(c)
print(flag)
# afctf{R54_|5_$0_B0rin9}

模不互质

当题目给出多个n，多个c，但只给出一个e，我们可以考虑模不互质攻击

q = gcd(n1,n2)

ezrsa

这题是将一个同一个密文，用不同的模，相同的e加密了两次

import math
from gmpy2 import invert
from Crypto.Util.number import *


n1 = 103835296409081751860770535514746586815395898427260334325680313648369132661057840680823295512236948953370895568419721331170834557812541468309298819497267746892814583806423027167382825479157951365823085639078738847647634406841331307035593810712914545347201619004253602692127370265833092082543067153606828049061
n2 = 115383198584677147487556014336448310721853841168758012445634182814180314480501828927160071015197089456042472185850893847370481817325868824076245290735749717384769661698895000176441497242371873981353689607711146852891551491168528799814311992471449640014501858763495472267168224015665906627382490565507927272073
e = 65537
flag =
c = pow(flag,e,n1)
c = pow(c,e,n2)
print(c)

#c=89624483360276074856011726888512095222773886375935390632322243611990748676661578370812870896647725693055942461208179974507367326886187428769565464612599398828896896815588677526117803992483614423139896898597788550271683093797162530843285205405331463405761603448815504547110859369661150095379164767159123704212

import math
import gmpy2
from Crypto.Util.number import *

e = 65537
c = 89624483360276074856011726888512095222773886375935390632322243611990748676661578370812870896647725693055942461208179974507367326886187428769565464612599398828896896815588677526117803992483614423139896898597788550271683093797162530843285205405331463405761603448815504547110859369661150095379164767159123704212
n1 = 103835296409081751860770535514746586815395898427260334325680313648369132661057840680823295512236948953370895568419721331170834557812541468309298819497267746892814583806423027167382825479157951365823085639078738847647634406841331307035593810712914545347201619004253602692127370265833092082543067153606828049061
n2 = 115383198584677147487556014336448310721853841168758012445634182814180314480501828927160071015197089456042472185850893847370481817325868824076245290735749717384769661698895000176441497242371873981353689607711146852891551491168528799814311992471449640014501858763495472267168224015665906627382490565507927272073


p = gmpy2.gcd(n1,n2)
q2 = n2 // p
q1 = n1 // p

d1 = gmpy2.invert(e,(p-1)*(q2-1))
m1 = pow(c,d1,n2)

d2 = gmpy2.invert(e,(p-1)*(q1-1))
m2 = pow(m1,d2,n1)
print(long_to_bytes(m2))
# flag{CMCTF_CRYPTO_RsA2}

dp泄露

RSA2 (dp泄露)

题目给了个dp，也不知道是啥，继续因式分解，求p和q

其中解出来的密文m需要用Crypto.Util.number的库中long_to_bytes()函数

import gmpy2
from Crypto.Util.number import *
e = 65537
n = 248254007851526241177721526698901802985832766176221609612258877371620580060433101538328030305219918697643619814200930679612109885533801335348445023751670478437073055544724280684733298051599167660303645183146161497485358633681492129668802402065797789905550489547645118787266601929429724133167768465309665906113
c = 140423670976252696807533673586209400575664282100684119784203527124521188996403826597436883766041879067494280957410201958935737360380801845453829293997433414188838725751796261702622028587211560353362847191060306578510511380965162133472698713063592621028959167072781482562673683090590521214218071160287665180751
p = 13468634736343473907717969603434376212206335187555458742257940406618189481177835992217885676243155145465521141546915941147336786447889325606555333350540003
q = 18432009829596386103558375461387837845170621179295293289126504231317130550979989727125205467379713835047300158256398009229511746203459540859429194971855371
d = gmpy2.invert(e,(p-1)*(q-1))
m = int(pow(c,d,n))
print(long_to_bytes(m))

–更新–

查看前方是否可导？大佬的博客之后才发现，dp是用来帮助n来分解p和q的，也就是可以通过dp求得p

已知：
ed ≡ 1 (mod (p-1)(q-1))
# d 是e关于φ(n)的模逆，所以ed = 1 mod (p-1)(q-1)
# ed = k(p-1)(q-1) +1

dp = d%(p-1)
# d = k1*(p-1) + dp
# ed = ek1(p-1) + edp

所以：
k2(p-1)(q-1) + ek1(p-1) + e*dp = 1

两边对p-1求余：
e*dp % (p-1) = 1  

所以：
e * dp = k(p-1) +1 
# p = (e * dp - 1 / k) + 1

k = (e * dp - 1)/(p - 1)
  = e(dp/p-1) - 1/(p-1)
#所以 k < e

直接引用大佬的原话：

“由dp=d%(p-1)我们可以知道dp<p-1,因此我们很容易得到k的上限要小于e，因此只需要遍历range(1,e) ,若n整除p,即可得到p,从而结束循环。”

我们已知e和dp，我们需要遍历循环k，使得k能被（e*dp - 1）整除，若当前k值满足条件，则 p = k + 1

引用大佬代码：

import  gmpy2
import  rsa
import  binascii
# from Crypto.Util.number import *
p=0
e=65537
c = 140423670976252696807533673586209400575664282100684119784203527124521188996403826597436883766041879067494280957410201958935737360380801845453829293997433414188838725751796261702622028587211560353362847191060306578510511380965162133472698713063592621028959167072781482562673683090590521214218071160287665180751
dp=905074498052346904643025132879518330691925174573054004621877253318682675055421970943552016695528560364834446303196939207056642927148093290374440210503657
n=248254007851526241177721526698901802985832766176221609612258877371620580060433101538328030305219918697643619814200930679612109885533801335348445023751670478437073055544724280684733298051599167660303645183146161497485358633681492129668802402065797789905550489547645118787266601929429724133167768465309665906113
temp=dp*e
for i in range(1,e) :
    if (temp-1)%i==0:
        # i+1 就是 p的值
        x=(temp-1)//i+1
        y=n%x
        if y==0:
            p=x
            break

#'//'代表向下取整,'/'得到的是浮点数
q=n//p
d=gmpy2.invert(e,(p-1)*(q-1))
key=rsa.PrivateKey(n,e,d,p,q)
m=pow(c,d,n)
#unhexlify()的作用是返回16进制数对应的字符串
print(binascii.unhexlify(hex(m)[2:]))
#print(long_to_bytes(m))

共模攻击

1ABlades的这篇文章讲的非常详细

假设有一条信息m，使用公钥加密信息（使用了相同的模数n):

1 2	c1 = m e1 mod n c2 = m e2 mod n

就可以用密钥d1，d2来求解

1 2	m = c1 d1 mod n m = c2 d2 mod n

因为e1,e2互质，即

1	gcd(e1,e2)=1

根据扩展欧几里得算法（如果gcd(a, b) = c，则存在x, y，使得c = ax + by。）

则有

1	e1s1 + e2s2 = 1

于是我们就能得到以下的公式：

1	c1 ** s1 * c2 ** s2= m

推算过程：

(c1 ** s1 * c2 ** s2) mod n = ((m ** e1 mod n) ** s1 * (m ** e2 mod n) ** s2) mod n
(c1 ** s1 * c2 ** s2) mod n = (m ** (e1 ** s1 + e2 ** s2)) mod n
(c1 ** s1 * c2 ** s2) mod n = (m ** (1)) mod n
 c1 ** s1 * c2 ** s2= m

并且可以知道s1/s2皆为整数，且一正一负

RSA3 (共模攻击)

题目中给出了两个e和两个c,一个n

了解原理之后，直接上代码：

import  gmpy2
from Crypto.Util import number

#扩展欧几里得算法
def exgcd(m, n, x, y):
    if n == 0:
        x = 1
        y = 0
        return (m, x, y)
    a1 = b = 1
    a = b1 = 0
    c = m
    d = n
    q = int(c / d)
    r = c % d
    while r:
        c = d
        d = r
        t = a1
        a1 = a
        a = t - q * a
        t = b1
        b1 = b
        b = t - q * b
        q = int(c / d)
        r = c % d
    x = a
    y = b
    return (d, x, y)

c1=22322035275663237041646893770451933509324701913484303338076210603542612758956262869640822486470121149424485571361007421293675516338822195280313794991136048140918842471219840263536338886250492682739436410013436651161720725855484866690084788721349555662019879081501113222996123305533009325964377798892703161521852805956811219563883312896330156298621674684353919547558127920925706842808914762199011054955816534977675267395009575347820387073483928425066536361482774892370969520740304287456555508933372782327506569010772537497541764311429052216291198932092617792645253901478910801592878203564861118912045464959832566051361
c2=18702010045187015556548691642394982835669262147230212731309938675226458555210425972429418449273410535387985931036711854265623905066805665751803269106880746769003478900791099590239513925449748814075904017471585572848473556490565450062664706449128415834787961947266259789785962922238701134079720414228414066193071495304612341052987455615930023536823801499269773357186087452747500840640419365011554421183037505653461286732740983702740822671148045619497667184586123657285604061875653909567822328914065337797733444640351518775487649819978262363617265797982843179630888729407238496650987720428708217115257989007867331698397
e1=11187289
e2=9647291
n=22708078815885011462462049064339185898712439277226831073457888403129378547350292420267016551819052430779004755846649044001024141485283286483130702616057274698473611149508798869706347501931583117632710700787228016480127677393649929530416598686027354216422565934459015161927613607902831542857977859612596282353679327773303727004407262197231586324599181983572622404590354084541788062262164510140605868122410388090174420147752408554129789760902300898046273909007852818474030770699647647363015102118956737673941354217692696044969695308506436573142565573487583507037356944848039864382339216266670673567488871508925311154801
ans=exgcd(e1,e2,0,0)
s1=ans[1]
s2=ans[2]

#powmod()函数,分数取模也可以直接算
m=(gmpy2.powmod(c1,s1,n)*gmpy2.powmod(c2,s2,n))%n

print(number.long_to_bytes(m))

参考链接

RSA & what (共模攻击+base64隐写)

import  gmpy2
from Crypto.Util.number import *
import base64

#扩展欧几里得算法
def exgcd(m, n, x, y):
    if n == 0:
        x = 1
        y = 0
        return (m, x, y)
    a1 = b = 1
    a = b1 = 0
    c = m
    d = n
    q = int(c / d)
    r = c % d
    while r:
        c = d
        d = r
        t = a1
        a1 = a
        a = t - q * a
        t = b1
        b1 = b
        b = t - q * b
        q = int(c / d)
        r = c % d
    x = a
    y = b
    return (d, x, y)

n=785095419718268286866508214304816985447077293766819398728046411166917810820484759314291028976498223661229395009474063173705162627037610993539617751905443039278227583504604808251931083818909467613277587874545761074364427549966555519371913859875313577282243053150056274667798049694695703660313532933165449312949725581708965417273055582216295994587600975970124811496270080896977076946000102701030260990598181466447208054713391526313700681341093922240317428173599031624125155188216489476825606191521182034969120343287691181300399683515414809262700457525876691808180257730351707673660380698973884642306898810000633684878715402823143549139850732982897459698089649561190746850698130299458080255582312696873149210028240898137822888492559957665067936573356367589784593119016624072433872744537432005911668494455733330689385141214653091888017782049043434862620306783436169856564175929871100669913438980899219579329897753233450934770193915434791427728636586218049874617231705308003720066269312729135764175698611068808404054125581540114956463603240222497919384691718744014002554201602395969312999994159599536026359879060218056496345745457493919771337601177449899066579857630036350871090452649830775029695488575574985078428560054253180863725364147
e1 = 1697
e2 = 599
c1_1 = 412629526163150748619328091306742267675740578011800062477174189782151273970783531227579758540364970485350157944321579108232221072397135934034064481497887079641131808838242743811511451355024436983050572020925065644355566434625618133203024215941534926113892937988520918939061441606915556516246057349589921494351383160036280826024605351878408056180907759973804117263002554923041750587548819746346813966673034182913325507826219961923932100526305289894965216608254252188398580139545189681875824089456195044984585824938384521905334289906422454152976834867304693292466676355760173232407753256256317546190171995276258924613533179898467683358934751999655196790168438343198229183747091108262988777659858609744709324571850262293294975336628234767258858873839342596887193772615000676401522431518310648303975593582965021189182246986957349253156736526071639973844039068996404290548474640668851856078201093335425412842295604919065487301340901573809617549185106072798799159726375235125260509158832996701927878713084753334549129580912412168594170659605421750204835970231909591063407612779337478065175988365401590396247576709343727196106058477166945670117868989025903023998142850338956985816131805349549059377047477131270847579095628384569645636821650
c1_2 = 494644347943710545224678831941589086572700792465459558770782213550069709458568349686998660541810166872034041584767487150140111151788221460027897193248273461607411027815984883969396220626358625041781558277804930212654296704055890683796941327712758797770820006623289146990000114915293539639766846910274034245607746230740851938158390562286057002223177609606376329007676845450142537930798148258428701466415483232670659815791064681384406494388237742330786225557303988025468036820082959712050733095860546860468575857084616069132051094882919253745234762029759124776348047587755897123575123506976140900565238840752841856713613368250071926171873213897914794115466890719123299469964019450899291410760762179836946570945555295288184698184555018368687708432612286248476073758067175481771199066581572870175460016017100414479346437034291784837132240891321931601494414908927713208448927221095745802380014441841139882391378410438764884597938773868771896252329517440068673532468372840830510218585255432000690265226016573313570977945083879214961394087065558376158826938257664840570952233832852869328785568175434516247720356520242602299510374317488182738732700078879665745909603766482100138001417023680647717824323143388857817595766172152883484274718248
c1_3 = 152942283599728307168144137370127212672611894072038732126041098102628831053000986759260271210671922070555948023688596575415822984026159010574404359474670428678518262175033880513984372909748992727828381694416776740981021730545374002974037896534944567124543272737618380646771071804878796585983783360553761828325817820260204820004421979881871027255562690952334900616675606524933557440263648233514757200263521499508373975003431306847453046714027687108396945719803444444954079308404947126216395526551292104722047878178373207886033071857277857997932255251315982837892164421298202073945919187779856785892717251746704537315003771369737854896595170485152591013676942418134278534037654467840633528916812275267230155352077736583130992587670941654695382287023971261529987384520843829695778029311786431227409189019205818351911572757145556993606643464336196802350204616056286497246016800105003143046120608673496196758720552776772796609670537056331996894322779267635281472481559819839042424017171718303214059720568484939239370144038161541354254182769979771948759413102933987773401644506930205164891773826513161783736386604783484446345744957119469799231796368324927570694496679453313927562345656690240414624431304646248599226046524702364131095964335
c1_4 = 79717988936247951265489157583697956031893477858854186991051529161879478488281744062318600470906120960002282886511477294555606503083169449335174864424180701080203993329996226566203834693869525797695969610065991941396723959032680019082506816443041598300477625793433080664346470586416385854692124426348587211026568667694805849554780794033764714016521711467557284846737236374990121316809833819996821592832639024026411520407330206281265390130763948165694574512140518775603040182029818771866749548761938870605590174330887949847420877829240131490902432602005681085180807294176837646062568094875766945890382971790015490163385088144673549085079635083262975154206269679142412897438231719704933258660779310737302680265445437771977749959110744959368586293082016067927548564967400845992380076107522755566531760628823374519718763740378295585535591752887339222947397184116326706799921515431185636740825707782742373783475781052674257292910213843986132987466810027275052416774693363446184518901899202502828670309452622347532932678874990809930682575738653876289384151496807194146308614368821006660626870989784697045160231069428458961107751207771093777394616856305293335603892178327520756554333365975114235981173451368131680404850832773147333013716920
c1_5 = 123111353650401158556639983459870663057297871992927053886971224773529636525110628183715748795987525113177540092814119928708272290370336537110381023134637759740716140969662183269370676630325583385284994943164692397459103195434968057377474610500216801375394703781249039351368816958227409657934091741509357152328382960684515093945552479461382281913961956745154260686029997827565075768703774895750561575155143606297116391666385705899138085693913246313778033627210312268959737394553510894720099165193981333775907531107232556909478156441457899797515694348816961762796703443502856101079430585547997496001098926600499728389113862894833789669213630332988693669889340482430613291490613803204484751470676686041002772556117213612152322606737150858116122936539131795111263513114569794532805886643087299918196635113037777138666914296986040549274559835214505300618256105508764026461518876579387159881983544667258537064954616097750399839661065797883103731694314852301848272092388637114950059216922969842082648527035538090054093890365647676119748995243416337805666557501345234056968476142608491830438065401219751688687373709390057521910942736632126729711606256158399963682990881473178216060827021373776598901281958527655543318413664277921492723185984
c1_6 = 36869806815936046911848195817405817350259890871483063184373728397968909458432625046025376290214729914038387534731762237978339011724858818860181178811639468996206294711495853807311240013786226884265118119546377272154555615363105236192878292703331473547623021744317034819416624562896226194523639793573028006666236271812390759036235867495803255905843636447252225413871038762657801345647584493917576263471587347202664391908570140389126903204602391093990827188675090199750617303773574821926387194478875191828814971296674530519321530805302667925998711835019806761133078403281404889374663875077339168901297819436499920958268483684335998301056068380228873524800383911402490807139268964095165069610454677558808756444381542173782815227920906224931028457073652453777424387873533280455944646592996920617956675786286711447540353883400282402551158169958389450168079568459656526911857835375748015814860506707921852997096156275804955989964215077733621769938075413007804223217091604613132253046399456747595300404564172224333936405545921819654435437072133387523533568472443532200069133022979195685683508297337961701169394794966256415112246587706103819620428258245999539040721929317130088874161577093962579487428358736401687123174207198251449851429295

c2_1 = 592169079372093727306100216011395857825646323934289480976073629037543922902098120901138454462177159996376654176248238979132528728327590301098966139983157980612320563496546128644967731000716697705104079039156276714872147463350811303393260622707024952543509891692246246277965823414460326811240048060543656588688604452353899779068825120910282167004715339763187734797180326976132213325054697165320479166356562518029805927741656605174809726397565772271562066078076105491745903986597877400370206718954975288721072048333678609055008135809089304229015364348490924974097403734627265297637171818849461766523691595241613878709865506436588268999163342945070495338153600520537498539457396582804692959296612715752573140296135784933206146091436617979599749774330699946637591406356289409716084034451049094715202196203486088368791744107629271647320273259836915312794297246589501008666299165717722507702866033454215783240025504356157664454861755286285777763585177751796252655008206383024707883077513745863312079349790275094080707502392866946325796914450602264462588722052297430827681750827349094323968337670311272933785838850649376115667223821665435911506351891489985627506615492005617098615432522564204152887767244129985681083657783356557756654335186
c2_2 = 373940646416832740878733255707567753033716583448402000789202767511920210382830343955553654111486728333980557319799362514960627879016797491389812007768832730979916230647641872759001906846747977631675704310179448857128160385701185892914523053669366534408863734305635222625590986006420486092550427301086984563126480814987024980594613542978310129247678826691418335300577577527951623696426435497835228167084738007750914270251001921329521479047662848650808989996085600197309361410863238526802127877523767262921515150984998560136647154865791163316503073285223966216441025637452229043510097323724381056976302288136843260163922706692913035222445496716008888946581535004546355744211680390731257309941902587303353139951102244865270295414474488798335404630458489706639805186573874814586736746232358849677477533671968344154242963289415569487579895910660999043578737461300406937828924818002658292769882181668784501439254131996848948120781562158861495883827848139425862249576454689133681009549361314460818658995959098228995702202268649635363105549975932395335076521137604288520082040121286614922986554652700056148966514178935952363036963217619879899671383604638416567950421350546204434902113156720006282720889591288850271076074941927715678306057176
c2_3 = 527630926460622936571385649841758214453416849039412401087443444317101857090904711485538107058823056085840539073345920792871368232355475394571098380596835468509997340505604333730547799560998822989747473780307779717715522787724471724766494090783971030594671013168209717686720448579582618378459567979027822271918653169622428153856198907810040224340270362413432495029672123261375400927159831537760709974778708160583252613784358234858583174544777979242887938827573604837766801998381379999076416444683891078093889686055482709838668356120916040352123019019255084513769603803814947774554028717814638951416291274696771515474086351482107953150253616922787262398450376249126999644026382478413080973933173079111305142716133389111399235545279259017424722601848670061556859163943895466553927946412523750166582734005733378328468250568944945912238495877929717101722314678120172228493787964904072583905721074766711732215815561012960394537195757832959268603775112932862105945720853959285187521763557915356428113876893276879775603217718981852114599706699524551973934242045743122744146361596971245034059345915315495232135483464496114770357536576200511490922413208178149869347802988786513451486411409887164516065062084917556120712465074206435831498113605
c2_4 = 8786437178698940322877889807009957616777351844979869726962356553244050911283984280960665761649310895230455072977431415102053987735969326553978994853162483051544656873294555116009995592043183070208706258164840540599577072097104139505857517663273929851202628854185356185647194933800084230503413037858893307713037149307477830536758283681093517617820169181420796105338681582230788318108428132051793761014952837330456262272828627355701464740578197966332613127307037255647286823496355917642353327912440019621838870388091824748629637425759125214639885130163183752378908729773517053259212525494555880921052679512582051516604297098204363525081039382358483926727008679327719083138865969291911863630382097160230960738043575559330264018212774424527719153248563876760067931499029384228993253862501939337758514377472011933279273181144830381169849387893799390755052093069179605579485710343655570028592595882436632426527654452895431758715126580164902410286422637215098476316042367916779431052267545769495994723721129943616294879642305545894912914632980455031755879087401575310699765408473606166727137934224515998416625122213056208800095077933103150699272650116151674702438463062734472714004926103668378506804002740045547964716693536349447660850580
c2_5 = 205314962204511500352858372254132533167549960825498949618514841570703199264867431580754674275990554478140637041427842111391746883257447120035947621456863890934062044010795443059281736346976175772415034838334682726635263432655537852942177334888025283748611576171534251461847349566505628290587224150869640386437623371249743165260396675220683302142805646368906930575140628610003919131999295855501215111393294818218799982703289304596989070475000081175510085432290264502023736899104746316830742226946395027029820825791831870857382647221322734605026210073093918331247494307555600335550942340526536281372036612138713881098866303169425501998978400008829873080965592009371176208668290074288903681417933657472279670688597862835627506340169978450918788539270346340385928840299573889292189531738082166408734046381423516467694328971385421907314814283489322619386570046183556572383980777277173349209330683424343658179781015072259378576130442222984963071166207642585589822061597282467850868050737957726423713761694231879497037175627546427449730638216214828463003483408928375620315193290871300316930139260521382533279767663839278693750409419493280753368451508802658272220767624766390639285308433607255253282702383762149755935518922075584637512494819
c2_6 = 271453634732502613378948161256470991260052778799128789839624515809143527363206813219580098196957510291648493698144497567392065251244844074992734669490296293997386198359280316655904691639367482203210051809125904410431506925238374843856343243276508280641059690938930957474434518308646618959004216831130099873532714372402117796666560677624822509159287675432413016478948594640872091688482149004426363946048517480052906306290126242866034249478040406351940088231081456109195799442996799641647167552689564613346415247906852055588498305665928450828756152103096629274760601528737639415361467941349982213641454967962723875032638267311935042334584913897338553953961877439389588793074211502597238465542889335363559052368180212013206172712561221352833891640659020253527584706465205486408990762759230842192028381048563437724528409174790022752557512795782713125166158329880702730769957185428522011430144840232256419113631679343171680631630775266488738173707357123139368825087043785842169049943237537188129367275730984789479909103397937113837824575137021012333461552176687570010445744268373840742899299977372834041925102853718964831225250407279578465008537542659673685686242773379131904890865110699190451534445434533919127658976874721029586168106207



c1=412629526163150748619328091306742267675740578011800062477174189782151273970783531227579758540364970485350157944321579108232221072397135934034064481497887079641131808838242743811511451355024436983050572020925065644355566434625618133203024215941534926113892937988520918939061441606915556516246057349589921494351383160036280826024605351878408056180907759973804117263002554923041750587548819746346813966673034182913325507826219961923932100526305289894965216608254252188398580139545189681875824089456195044984585824938384521905334289906422454152976834867304693292466676355760173232407753256256317546190171995276258924613533179898467683358934751999655196790168438343198229183747091108262988777659858609744709324571850262293294975336628234767258858873839342596887193772615000676401522431518310648303975593582965021189182246986957349253156736526071639973844039068996404290548474640668851856078201093335425412842295604919065487301340901573809617549185106072798799159726375235125260509158832996701927878713084753334549129580912412168594170659605421750204835970231909591063407612779337478065175988365401590396247576709343727196106058477166945670117868989025903023998142850338956985816131805349549059377047477131270847579095628384569645636821650
c2=592169079372093727306100216011395857825646323934289480976073629037543922902098120901138454462177159996376654176248238979132528728327590301098966139983157980612320563496546128644967731000716697705104079039156276714872147463350811303393260622707024952543509891692246246277965823414460326811240048060543656588688604452353899779068825120910282167004715339763187734797180326976132213325054697165320479166356562518029805927741656605174809726397565772271562066078076105491745903986597877400370206718954975288721072048333678609055008135809089304229015364348490924974097403734627265297637171818849461766523691595241613878709865506436588268999163342945070495338153600520537498539457396582804692959296612715752573140296135784933206146091436617979599749774330699946637591406356289409716084034451049094715202196203486088368791744107629271647320273259836915312794297246589501008666299165717722507702866033454215783240025504356157664454861755286285777763585177751796252655008206383024707883077513745863312079349790275094080707502392866946325796914450602264462588722052297430827681750827349094323968337670311272933785838850649376115667223821665435911506351891489985627506615492005617098615432522564204152887767244129985681083657783356557756654335186
e1=1697
e2=599

ans=exgcd(e1,e2,0,0)
s1=ans[1]
s2=ans[2]

c1 = [c1_1,c1_2,c1_3,c1_4,c1_5,c1_6]
c2 = [c2_1,c2_2,c2_3,c2_4,c2_5,c2_6]

#powmod()函数,分数取模也可以直接算
bases = ""
for i in range(len(c1)):
    m = (gmpy2.powmod(c1[i],s1,n)*gmpy2.powmod(c2[i],s2,n)) % n
    bases += str(long_to_bytes(m),"utf-8")

# print(flag.replace("\n","','"))
bases = ['VEhJUz==','RkxBR3==','SVN=','SElEREVOLo==','Q0FO','WU9V','RklORM==','SVT=','T1VUP4==','RE8=','WU9V','S05PV9==','QkFTRTY0P5==','WW91bmdD','VEhJTku=','WU9V','QVJF','Tk9U','VEhBVE==','RkFNSUxJQVI=','V0lUSO==','QkFTRTY0Lh==','QmFzZTY0','aXO=','YW==','Z3JvdXA=','b2b=','c2ltaWxhcn==','YmluYXJ5LXRvLXRleHR=','ZW5jb2Rpbme=','c2NoZW1lc0==','dGhhdD==','cmVwcmVzZW50','YmluYXJ5','ZGF0YW==','aW5=','YW6=','QVNDSUl=','c3RyaW5n','Zm9ybWF0','Ynk=','dHJhbnNsYXRpbmd=','aXS=','aW50b1==','YT==','cmFkaXgtNjQ=','cmVwcmVzZW50YXRpb24u','VGhl','dGVybc==','QmFzZTY0','b3JpZ2luYXRlc8==','ZnJvbd==','YY==','c3BlY2lmaWN=','TUlNRT==','Y29udGVudI==','dHJhbnNmZXI=','ZW5jb2Rpbmcu','VGhl','cGFydGljdWxhct==','c2V0','b2b=','NjR=','Y2hhcmFjdGVyc5==','Y2hvc2Vu','dG+=','cmVwcmVzZW50','dGhl','NjQ=','cGxhY2UtdmFsdWVz','Zm9y','dGhl','YmFzZd==','dmFyaWVz','YmV0d2Vlbt==','aW1wbGVtZW50YXRpb25zLp==','VGhl','Z2VuZXJhbI==','c3RyYXRlZ3n=','aXO=','dG9=','Y2hvb3Nl','NjR=','Y2hhcmFjdGVyc5==','dGhhdA==','YXJl','Ym90aN==','bWVtYmVyc5==','b2a=','YS==','c3Vic2V0','Y29tbW9u','dG8=','bW9zdM==','ZW5jb2RpbmdzLA==','YW5k','YWxzb8==','cHJpbnRhYmxlLg==','VGhpc9==','Y29tYmluYXRpb25=','bGVhdmVz','dGhl','ZGF0YW==','dW5saWtlbHk=','dG/=','YmV=','bW9kaWZpZWS=','aW5=','dHJhbnNpdE==','dGhyb3VnaN==','aW5mb3JtYXRpb26=','c3lzdGVtcyw=','c3VjaN==','YXM=','RS1tYWlsLD==','dGhhdA==','d2VyZQ==','dHJhZGl0aW9uYWxseQ==','bm90','OC1iaXQ=','Y2xlYW4uWzFd','Rm9y','ZXhhbXBsZSw=','TUlNRSdz','QmFzZTY0','aW1wbGVtZW50YXRpb24=','dXNlcw==','QahDWiw=','YahDeiw=','YW5k','MKhDOQ==','Zm9y','dGhl','Zmlyc3Q=','NjI=','dmFsdWVzLg==','T3RoZXI=','dmFyaWF0aW9ucw==','c2hhcmU=','dGhpcw==','cHJvcGVydHk=','YnV0','ZGlmZmVy','aW4=','dGhl','c3ltYm9scw==','Y2hvc2Vu','Zm9y','dGhl','bGFzdA==','dHdv','dmFsdWVzOw==','YW4=','ZXhhbXBsZQ==','aXM=','VVRGLTcu']

flag = ""
for i in bases:
    print(str(base64.b64decode(i))[2:-1],end = " ")
# THIS FLAG IS HIDDEN. CAN YOU FIND IT OUT? DO YOU KNOW BASE64? YoungC THINK YOU ARE NOT THAT FAMILIAR WITH BASE64. Base64 is a group of similar binary-to-text encoding schemes that represent binary data in an ASCII string format by translating it into a radix-64 representation. The term Base64 originates from a specific MIME content transfer encoding. The particular set of 64 characters chosen to represent the 64 place-values for the base varies between implementations. The general strategy is to choose 64 characters that are both members of a subset common to most encodings, and also printable. This combination leaves the data unlikely to be modified in transit through information systems, such as E-mail, that were traditionally not 8-bit clean.[1] For example, MIME's Base64 implementation uses A\xa8CZ, a\xa8Cz, and 0\xa8C9 for the first 62 values. Other variations share this property but differ in the symbols chosen for the last two values; an example is UTF-7.

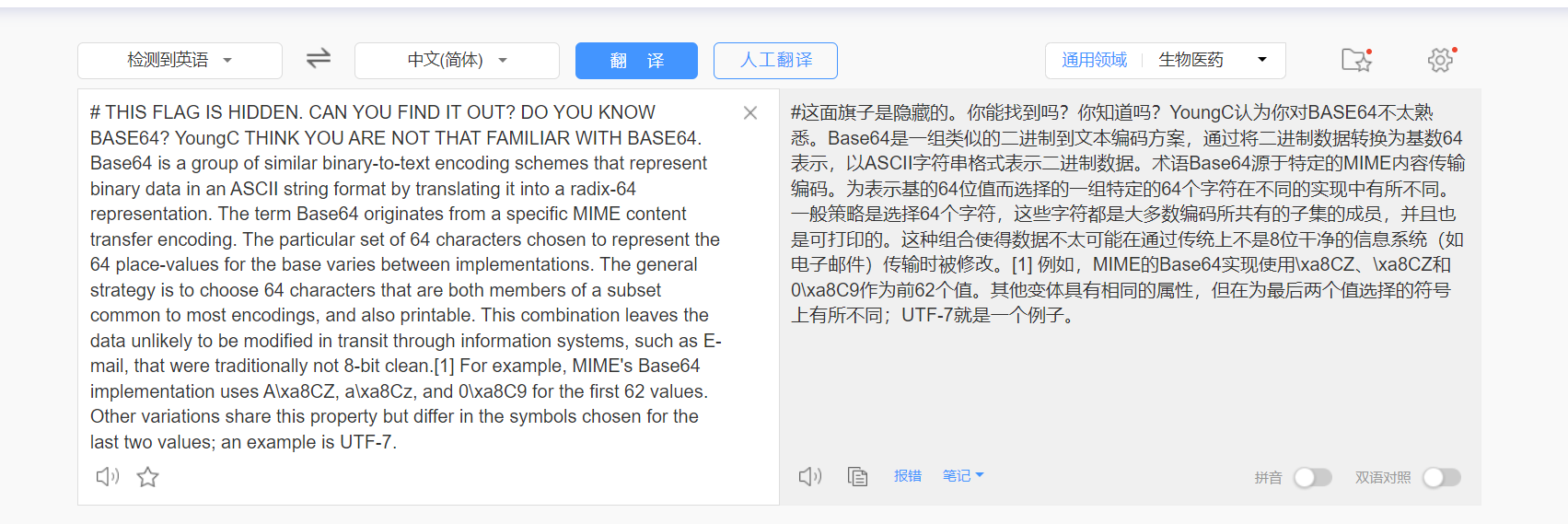
以为通过共模攻击求解bases，再base64解码就可以了，没想到还有隐藏的flag，没辙了

–更新–

https://blog.csdn.net/qq_41956187/article/details/105592471

没想到竟然有base64隐写，颠覆了我的认知，怪不得会有那么多的换行……

完整代码：

import  gmpy2
from Crypto.Util.number import *
import base64

#扩展欧几里得算法
def exgcd(m, n, x, y):
    if n == 0:
        x = 1
        y = 0
        return (m, x, y)
    a1 = b = 1
    a = b1 = 0
    c = m
    d = n
    q = int(c / d)
    r = c % d
    while r:
        c = d
        d = r
        t = a1
        a1 = a
        a = t - q * a
        t = b1
        b1 = b
        b = t - q * b
        q = int(c / d)
        r = c % d
    x = a
    y = b
    return (d, x, y)

n=785095419718268286866508214304816985447077293766819398728046411166917810820484759314291028976498223661229395009474063173705162627037610993539617751905443039278227583504604808251931083818909467613277587874545761074364427549966555519371913859875313577282243053150056274667798049694695703660313532933165449312949725581708965417273055582216295994587600975970124811496270080896977076946000102701030260990598181466447208054713391526313700681341093922240317428173599031624125155188216489476825606191521182034969120343287691181300399683515414809262700457525876691808180257730351707673660380698973884642306898810000633684878715402823143549139850732982897459698089649561190746850698130299458080255582312696873149210028240898137822888492559957665067936573356367589784593119016624072433872744537432005911668494455733330689385141214653091888017782049043434862620306783436169856564175929871100669913438980899219579329897753233450934770193915434791427728636586218049874617231705308003720066269312729135764175698611068808404054125581540114956463603240222497919384691718744014002554201602395969312999994159599536026359879060218056496345745457493919771337601177449899066579857630036350871090452649830775029695488575574985078428560054253180863725364147
e1 = 1697
e2 = 599
c1_1 = 412629526163150748619328091306742267675740578011800062477174189782151273970783531227579758540364970485350157944321579108232221072397135934034064481497887079641131808838242743811511451355024436983050572020925065644355566434625618133203024215941534926113892937988520918939061441606915556516246057349589921494351383160036280826024605351878408056180907759973804117263002554923041750587548819746346813966673034182913325507826219961923932100526305289894965216608254252188398580139545189681875824089456195044984585824938384521905334289906422454152976834867304693292466676355760173232407753256256317546190171995276258924613533179898467683358934751999655196790168438343198229183747091108262988777659858609744709324571850262293294975336628234767258858873839342596887193772615000676401522431518310648303975593582965021189182246986957349253156736526071639973844039068996404290548474640668851856078201093335425412842295604919065487301340901573809617549185106072798799159726375235125260509158832996701927878713084753334549129580912412168594170659605421750204835970231909591063407612779337478065175988365401590396247576709343727196106058477166945670117868989025903023998142850338956985816131805349549059377047477131270847579095628384569645636821650
c1_2 = 494644347943710545224678831941589086572700792465459558770782213550069709458568349686998660541810166872034041584767487150140111151788221460027897193248273461607411027815984883969396220626358625041781558277804930212654296704055890683796941327712758797770820006623289146990000114915293539639766846910274034245607746230740851938158390562286057002223177609606376329007676845450142537930798148258428701466415483232670659815791064681384406494388237742330786225557303988025468036820082959712050733095860546860468575857084616069132051094882919253745234762029759124776348047587755897123575123506976140900565238840752841856713613368250071926171873213897914794115466890719123299469964019450899291410760762179836946570945555295288184698184555018368687708432612286248476073758067175481771199066581572870175460016017100414479346437034291784837132240891321931601494414908927713208448927221095745802380014441841139882391378410438764884597938773868771896252329517440068673532468372840830510218585255432000690265226016573313570977945083879214961394087065558376158826938257664840570952233832852869328785568175434516247720356520242602299510374317488182738732700078879665745909603766482100138001417023680647717824323143388857817595766172152883484274718248
c1_3 = 152942283599728307168144137370127212672611894072038732126041098102628831053000986759260271210671922070555948023688596575415822984026159010574404359474670428678518262175033880513984372909748992727828381694416776740981021730545374002974037896534944567124543272737618380646771071804878796585983783360553761828325817820260204820004421979881871027255562690952334900616675606524933557440263648233514757200263521499508373975003431306847453046714027687108396945719803444444954079308404947126216395526551292104722047878178373207886033071857277857997932255251315982837892164421298202073945919187779856785892717251746704537315003771369737854896595170485152591013676942418134278534037654467840633528916812275267230155352077736583130992587670941654695382287023971261529987384520843829695778029311786431227409189019205818351911572757145556993606643464336196802350204616056286497246016800105003143046120608673496196758720552776772796609670537056331996894322779267635281472481559819839042424017171718303214059720568484939239370144038161541354254182769979771948759413102933987773401644506930205164891773826513161783736386604783484446345744957119469799231796368324927570694496679453313927562345656690240414624431304646248599226046524702364131095964335
c1_4 = 79717988936247951265489157583697956031893477858854186991051529161879478488281744062318600470906120960002282886511477294555606503083169449335174864424180701080203993329996226566203834693869525797695969610065991941396723959032680019082506816443041598300477625793433080664346470586416385854692124426348587211026568667694805849554780794033764714016521711467557284846737236374990121316809833819996821592832639024026411520407330206281265390130763948165694574512140518775603040182029818771866749548761938870605590174330887949847420877829240131490902432602005681085180807294176837646062568094875766945890382971790015490163385088144673549085079635083262975154206269679142412897438231719704933258660779310737302680265445437771977749959110744959368586293082016067927548564967400845992380076107522755566531760628823374519718763740378295585535591752887339222947397184116326706799921515431185636740825707782742373783475781052674257292910213843986132987466810027275052416774693363446184518901899202502828670309452622347532932678874990809930682575738653876289384151496807194146308614368821006660626870989784697045160231069428458961107751207771093777394616856305293335603892178327520756554333365975114235981173451368131680404850832773147333013716920
c1_5 = 123111353650401158556639983459870663057297871992927053886971224773529636525110628183715748795987525113177540092814119928708272290370336537110381023134637759740716140969662183269370676630325583385284994943164692397459103195434968057377474610500216801375394703781249039351368816958227409657934091741509357152328382960684515093945552479461382281913961956745154260686029997827565075768703774895750561575155143606297116391666385705899138085693913246313778033627210312268959737394553510894720099165193981333775907531107232556909478156441457899797515694348816961762796703443502856101079430585547997496001098926600499728389113862894833789669213630332988693669889340482430613291490613803204484751470676686041002772556117213612152322606737150858116122936539131795111263513114569794532805886643087299918196635113037777138666914296986040549274559835214505300618256105508764026461518876579387159881983544667258537064954616097750399839661065797883103731694314852301848272092388637114950059216922969842082648527035538090054093890365647676119748995243416337805666557501345234056968476142608491830438065401219751688687373709390057521910942736632126729711606256158399963682990881473178216060827021373776598901281958527655543318413664277921492723185984
c1_6 = 36869806815936046911848195817405817350259890871483063184373728397968909458432625046025376290214729914038387534731762237978339011724858818860181178811639468996206294711495853807311240013786226884265118119546377272154555615363105236192878292703331473547623021744317034819416624562896226194523639793573028006666236271812390759036235867495803255905843636447252225413871038762657801345647584493917576263471587347202664391908570140389126903204602391093990827188675090199750617303773574821926387194478875191828814971296674530519321530805302667925998711835019806761133078403281404889374663875077339168901297819436499920958268483684335998301056068380228873524800383911402490807139268964095165069610454677558808756444381542173782815227920906224931028457073652453777424387873533280455944646592996920617956675786286711447540353883400282402551158169958389450168079568459656526911857835375748015814860506707921852997096156275804955989964215077733621769938075413007804223217091604613132253046399456747595300404564172224333936405545921819654435437072133387523533568472443532200069133022979195685683508297337961701169394794966256415112246587706103819620428258245999539040721929317130088874161577093962579487428358736401687123174207198251449851429295

c2_1 = 592169079372093727306100216011395857825646323934289480976073629037543922902098120901138454462177159996376654176248238979132528728327590301098966139983157980612320563496546128644967731000716697705104079039156276714872147463350811303393260622707024952543509891692246246277965823414460326811240048060543656588688604452353899779068825120910282167004715339763187734797180326976132213325054697165320479166356562518029805927741656605174809726397565772271562066078076105491745903986597877400370206718954975288721072048333678609055008135809089304229015364348490924974097403734627265297637171818849461766523691595241613878709865506436588268999163342945070495338153600520537498539457396582804692959296612715752573140296135784933206146091436617979599749774330699946637591406356289409716084034451049094715202196203486088368791744107629271647320273259836915312794297246589501008666299165717722507702866033454215783240025504356157664454861755286285777763585177751796252655008206383024707883077513745863312079349790275094080707502392866946325796914450602264462588722052297430827681750827349094323968337670311272933785838850649376115667223821665435911506351891489985627506615492005617098615432522564204152887767244129985681083657783356557756654335186
c2_2 = 373940646416832740878733255707567753033716583448402000789202767511920210382830343955553654111486728333980557319799362514960627879016797491389812007768832730979916230647641872759001906846747977631675704310179448857128160385701185892914523053669366534408863734305635222625590986006420486092550427301086984563126480814987024980594613542978310129247678826691418335300577577527951623696426435497835228167084738007750914270251001921329521479047662848650808989996085600197309361410863238526802127877523767262921515150984998560136647154865791163316503073285223966216441025637452229043510097323724381056976302288136843260163922706692913035222445496716008888946581535004546355744211680390731257309941902587303353139951102244865270295414474488798335404630458489706639805186573874814586736746232358849677477533671968344154242963289415569487579895910660999043578737461300406937828924818002658292769882181668784501439254131996848948120781562158861495883827848139425862249576454689133681009549361314460818658995959098228995702202268649635363105549975932395335076521137604288520082040121286614922986554652700056148966514178935952363036963217619879899671383604638416567950421350546204434902113156720006282720889591288850271076074941927715678306057176
c2_3 = 527630926460622936571385649841758214453416849039412401087443444317101857090904711485538107058823056085840539073345920792871368232355475394571098380596835468509997340505604333730547799560998822989747473780307779717715522787724471724766494090783971030594671013168209717686720448579582618378459567979027822271918653169622428153856198907810040224340270362413432495029672123261375400927159831537760709974778708160583252613784358234858583174544777979242887938827573604837766801998381379999076416444683891078093889686055482709838668356120916040352123019019255084513769603803814947774554028717814638951416291274696771515474086351482107953150253616922787262398450376249126999644026382478413080973933173079111305142716133389111399235545279259017424722601848670061556859163943895466553927946412523750166582734005733378328468250568944945912238495877929717101722314678120172228493787964904072583905721074766711732215815561012960394537195757832959268603775112932862105945720853959285187521763557915356428113876893276879775603217718981852114599706699524551973934242045743122744146361596971245034059345915315495232135483464496114770357536576200511490922413208178149869347802988786513451486411409887164516065062084917556120712465074206435831498113605
c2_4 = 8786437178698940322877889807009957616777351844979869726962356553244050911283984280960665761649310895230455072977431415102053987735969326553978994853162483051544656873294555116009995592043183070208706258164840540599577072097104139505857517663273929851202628854185356185647194933800084230503413037858893307713037149307477830536758283681093517617820169181420796105338681582230788318108428132051793761014952837330456262272828627355701464740578197966332613127307037255647286823496355917642353327912440019621838870388091824748629637425759125214639885130163183752378908729773517053259212525494555880921052679512582051516604297098204363525081039382358483926727008679327719083138865969291911863630382097160230960738043575559330264018212774424527719153248563876760067931499029384228993253862501939337758514377472011933279273181144830381169849387893799390755052093069179605579485710343655570028592595882436632426527654452895431758715126580164902410286422637215098476316042367916779431052267545769495994723721129943616294879642305545894912914632980455031755879087401575310699765408473606166727137934224515998416625122213056208800095077933103150699272650116151674702438463062734472714004926103668378506804002740045547964716693536349447660850580
c2_5 = 205314962204511500352858372254132533167549960825498949618514841570703199264867431580754674275990554478140637041427842111391746883257447120035947621456863890934062044010795443059281736346976175772415034838334682726635263432655537852942177334888025283748611576171534251461847349566505628290587224150869640386437623371249743165260396675220683302142805646368906930575140628610003919131999295855501215111393294818218799982703289304596989070475000081175510085432290264502023736899104746316830742226946395027029820825791831870857382647221322734605026210073093918331247494307555600335550942340526536281372036612138713881098866303169425501998978400008829873080965592009371176208668290074288903681417933657472279670688597862835627506340169978450918788539270346340385928840299573889292189531738082166408734046381423516467694328971385421907314814283489322619386570046183556572383980777277173349209330683424343658179781015072259378576130442222984963071166207642585589822061597282467850868050737957726423713761694231879497037175627546427449730638216214828463003483408928375620315193290871300316930139260521382533279767663839278693750409419493280753368451508802658272220767624766390639285308433607255253282702383762149755935518922075584637512494819
c2_6 = 271453634732502613378948161256470991260052778799128789839624515809143527363206813219580098196957510291648493698144497567392065251244844074992734669490296293997386198359280316655904691639367482203210051809125904410431506925238374843856343243276508280641059690938930957474434518308646618959004216831130099873532714372402117796666560677624822509159287675432413016478948594640872091688482149004426363946048517480052906306290126242866034249478040406351940088231081456109195799442996799641647167552689564613346415247906852055588498305665928450828756152103096629274760601528737639415361467941349982213641454967962723875032638267311935042334584913897338553953961877439389588793074211502597238465542889335363559052368180212013206172712561221352833891640659020253527584706465205486408990762759230842192028381048563437724528409174790022752557512795782713125166158329880702730769957185428522011430144840232256419113631679343171680631630775266488738173707357123139368825087043785842169049943237537188129367275730984789479909103397937113837824575137021012333461552176687570010445744268373840742899299977372834041925102853718964831225250407279578465008537542659673685686242773379131904890865110699190451534445434533919127658976874721029586168106207



c1=412629526163150748619328091306742267675740578011800062477174189782151273970783531227579758540364970485350157944321579108232221072397135934034064481497887079641131808838242743811511451355024436983050572020925065644355566434625618133203024215941534926113892937988520918939061441606915556516246057349589921494351383160036280826024605351878408056180907759973804117263002554923041750587548819746346813966673034182913325507826219961923932100526305289894965216608254252188398580139545189681875824089456195044984585824938384521905334289906422454152976834867304693292466676355760173232407753256256317546190171995276258924613533179898467683358934751999655196790168438343198229183747091108262988777659858609744709324571850262293294975336628234767258858873839342596887193772615000676401522431518310648303975593582965021189182246986957349253156736526071639973844039068996404290548474640668851856078201093335425412842295604919065487301340901573809617549185106072798799159726375235125260509158832996701927878713084753334549129580912412168594170659605421750204835970231909591063407612779337478065175988365401590396247576709343727196106058477166945670117868989025903023998142850338956985816131805349549059377047477131270847579095628384569645636821650
c2=592169079372093727306100216011395857825646323934289480976073629037543922902098120901138454462177159996376654176248238979132528728327590301098966139983157980612320563496546128644967731000716697705104079039156276714872147463350811303393260622707024952543509891692246246277965823414460326811240048060543656588688604452353899779068825120910282167004715339763187734797180326976132213325054697165320479166356562518029805927741656605174809726397565772271562066078076105491745903986597877400370206718954975288721072048333678609055008135809089304229015364348490924974097403734627265297637171818849461766523691595241613878709865506436588268999163342945070495338153600520537498539457396582804692959296612715752573140296135784933206146091436617979599749774330699946637591406356289409716084034451049094715202196203486088368791744107629271647320273259836915312794297246589501008666299165717722507702866033454215783240025504356157664454861755286285777763585177751796252655008206383024707883077513745863312079349790275094080707502392866946325796914450602264462588722052297430827681750827349094323968337670311272933785838850649376115667223821665435911506351891489985627506615492005617098615432522564204152887767244129985681083657783356557756654335186
e1=1697
e2=599

ans=exgcd(e1,e2,0,0)
s1=ans[1]
s2=ans[2]

c1 = [c1_1,c1_2,c1_3,c1_4,c1_5,c1_6]
c2 = [c2_1,c2_2,c2_3,c2_4,c2_5,c2_6]

#powmod()函数,分数取模也可以直接算
bases = ""
for i in range(len(c1)):
    m = (gmpy2.powmod(c1[i],s1,n)*gmpy2.powmod(c2[i],s2,n)) % n
    bases += str(long_to_bytes(m),"utf-8")

# print(flag.replace("\n","','"))
basesList = ['VEhJUz==','RkxBR3==','SVN=','SElEREVOLo==','Q0FO','WU9V','RklORM==','SVT=','T1VUP4==','RE8=','WU9V','S05PV9==','QkFTRTY0P5==','WW91bmdD','VEhJTku=','WU9V','QVJF','Tk9U','VEhBVE==','RkFNSUxJQVI=','V0lUSO==','QkFTRTY0Lh==','QmFzZTY0','aXO=','YW==','Z3JvdXA=','b2b=','c2ltaWxhcn==','YmluYXJ5LXRvLXRleHR=','ZW5jb2Rpbme=','c2NoZW1lc0==','dGhhdD==','cmVwcmVzZW50','YmluYXJ5','ZGF0YW==','aW5=','YW6=','QVNDSUl=','c3RyaW5n','Zm9ybWF0','Ynk=','dHJhbnNsYXRpbmd=','aXS=','aW50b1==','YT==','cmFkaXgtNjQ=','cmVwcmVzZW50YXRpb24u','VGhl','dGVybc==','QmFzZTY0','b3JpZ2luYXRlc8==','ZnJvbd==','YY==','c3BlY2lmaWN=','TUlNRT==','Y29udGVudI==','dHJhbnNmZXI=','ZW5jb2Rpbmcu','VGhl','cGFydGljdWxhct==','c2V0','b2b=','NjR=','Y2hhcmFjdGVyc5==','Y2hvc2Vu','dG+=','cmVwcmVzZW50','dGhl','NjQ=','cGxhY2UtdmFsdWVz','Zm9y','dGhl','YmFzZd==','dmFyaWVz','YmV0d2Vlbt==','aW1wbGVtZW50YXRpb25zLp==','VGhl','Z2VuZXJhbI==','c3RyYXRlZ3n=','aXO=','dG9=','Y2hvb3Nl','NjR=','Y2hhcmFjdGVyc5==','dGhhdA==','YXJl','Ym90aN==','bWVtYmVyc5==','b2a=','YS==','c3Vic2V0','Y29tbW9u','dG8=','bW9zdM==','ZW5jb2RpbmdzLA==','YW5k','YWxzb8==','cHJpbnRhYmxlLg==','VGhpc9==','Y29tYmluYXRpb25=','bGVhdmVz','dGhl','ZGF0YW==','dW5saWtlbHk=','dG/=','YmV=','bW9kaWZpZWS=','aW5=','dHJhbnNpdE==','dGhyb3VnaN==','aW5mb3JtYXRpb26=','c3lzdGVtcyw=','c3VjaN==','YXM=','RS1tYWlsLD==','dGhhdA==','d2VyZQ==','dHJhZGl0aW9uYWxseQ==','bm90','OC1iaXQ=','Y2xlYW4uWzFd','Rm9y','ZXhhbXBsZSw=','TUlNRSdz','QmFzZTY0','aW1wbGVtZW50YXRpb24=','dXNlcw==','QahDWiw=','YahDeiw=','YW5k','MKhDOQ==','Zm9y','dGhl','Zmlyc3Q=','NjI=','dmFsdWVzLg==','T3RoZXI=','dmFyaWF0aW9ucw==','c2hhcmU=','dGhpcw==','cHJvcGVydHk=','YnV0','ZGlmZmVy','aW4=','dGhl','c3ltYm9scw==','Y2hvc2Vu','Zm9y','dGhl','bGFzdA==','dHdv','dmFsdWVzOw==','YW4=','ZXhhbXBsZQ==','aXM=','VVRGLTcu']

flag = ""
for i in basesList:
    print(str(base64.b64decode(i))[2:-1],end = " ")
# THIS FLAG IS HIDDEN. CAN YOU FIND IT OUT? DO YOU KNOW BASE64? YoungC THINK YOU ARE NOT THAT FAMILIAR WITH BASE64. Base64 is a group of similar binary-to-text encoding schemes that represent binary data in an ASCII string format by translating it into a radix-64 representation. The term Base64 originates from a specific MIME content transfer encoding. The particular set of 64 characters chosen to represent the 64 place-values for the base varies between implementations. The general strategy is to choose 64 characters that are both members of a subset common to most encodings, and also printable. This combination leaves the data unlikely to be modified in transit through information systems, such as E-mail, that were traditionally not 8-bit clean.[1] For example, MIME's Base64 implementation uses A\xa8CZ, a\xa8Cz, and 0\xa8C9 for the first 62 values. Other variations share this property but differ in the symbols chosen for the last two values; an example is UTF-7. 


c = bytes(bases,encoding = "utf-8")
def get_base64_diff_value(s1, s2):
    base64chars = b'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/'
    res = 0
    for i in range(len(s2)):
        if s1[i] != s2[i]:
            return abs(base64chars.index(s1[i]) - base64chars.index(s2[i]))
    return res

def solve_stego():
    line=b''
    bin_str=''
    for i in c:
        k=long_to_bytes(i)
        if k==b'\n':
            steg_line = line
            norm_line = base64.b64encode(base64.b64decode(line))
            diff = get_base64_diff_value(steg_line, norm_line)
            #print(diff)
            pads_num = steg_line.count(b'=')
            if diff:
                bin_str += bin(diff)[2:].zfill(pads_num * 2)
            else:
                bin_str += '0' * pads_num * 2
            print(goflag(bin_str))
            line=b''
            continue
        line+=k

def goflag(bin_str):
    res_str = ''
    for i in range(0, len(bin_str), 8):
        res_str += chr(int(bin_str[i:i + 8], 2))
    return res_str

if __name__ == '__main__':
    solve_stego()
# flag{7c86d8f7d6de33a87f7f9d6b005ce640}

已知dp、dq

“一切以解题为目的的抄代码都是没有灵魂的，我们还是要从数学理论上去分析解决它，再去写代码。”

已知条件：
c ≡ m  **  e mod n 
m ≡ c  **  d mod n
φ(n) = (p-1)(q-1)
d*e ≡ 1 mod φ(n)
dp ≡ d mod (p-1)
dq ≡ d mod (q-1)

中国剩余定理：
m1 ≡ c  **  d mod P
m2 ≡ c  **  d mod q

经过各种推算:

1 2	m1 ≡ c dp mod p m2 ≡ c dq mod q

正常解法：

import gmpy2
I = gmpy2.invert(q,p)
mp = pow(c,dp,p)
mq = pow(c,dq,q)               #求幂取模运算

m = (((mp-mq)*I)%p)*q+mq       #求明文公式

print(hex(m))          #转为十六进制

RSA1 （已知dp、dq）

参考

import gmpy2
from Crypto.Util import number
p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229 
q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469 
c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852
dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929 
dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041 

I = gmpy2.invert(q,p)
mp = pow(c,dp,p)
mq = pow(c,dq,q)               #求幂取模运算

m = (((mp-mq)*I)%p)*q+mq       #求明文公式

print(number.long_to_bytes(m))          #long_to_bytes
# noxCTF{W31c0m3_70_Ch1n470wn}

低加密指数攻击

dangerous RSA （低加密指数攻击）

#n:  0x52d483c27cd806550fbe0e37a61af2e7cf5e0efb723dfc81174c918a27627779b21fa3c851e9e94188eaee3d5cd6f752406a43fbecb53e80836ff1e185d3ccd7782ea846c2e91a7b0808986666e0bdadbfb7bdd65670a589a4d2478e9adcafe97c6ee23614bcb2ecc23580f4d2e3cc1ecfec25c50da4bc754dde6c8bfd8d1fc16956c74d8e9196046a01dc9f3024e11461c294f29d7421140732fedacac97b8fe50999117d27943c953f18c4ff4f8c258d839764078d4b6ef6e8591e0ff5563b31a39e6374d0d41c8c46921c25e5904a817ef8e39e5c9b71225a83269693e0b7e3218fc5e5a1e8412ba16e588b3d6ac536dce39fcdfce81eec79979ea6872793L
#e:  0x3
#c:0x10652cdfaa6b63f6d7bd1109da08181e500e5643f5b240a9024bfa84d5f2cac9310562978347bb232d63e7289283871efab83d84ff5a7b64a94a79d34cfbd4ef121723ba1f663e514f83f6f01492b4e13e1bb4296d96ea5a353d3bf2edd2f449c03c4a3e995237985a596908adc741f32365
so,how to get the message?

因为c = m ** e%n，m = c ** d%n

当指数e很小的时候（通常为3），可以分两种情况来讨论

当m ** e<n：

c = m ** e

对c开e次根号
当m ** e>n:

m ** e = k * n+c

循环爆破k，使其满足条件

这边推荐使用gmpy2.iroot函数来开根号，这个函数的返回值为一个(x,y)元组，其中x为结果值，y为一个bool型变量，如果x为整数，y=True,否则y=False

import gmpy2
from Crypto.Util import number
e = 3
c = 0x10652cdfaa6b63f6d7bd1109da08181e500e5643f5b240a9024bfa84d5f2cac9310562978347bb232d63e7289283871efab83d84ff5a7b64a94a79d34cfbd4ef121723ba1f663e514f83f6f01492b4e13e1bb4296d96ea5a353d3bf2edd2f449c03c4a3e995237985a596908adc741f32365
n = 0x52d483c27cd806550fbe0e37a61af2e7cf5e0efb723dfc81174c918a27627779b21fa3c851e9e94188eaee3d5cd6f752406a43fbecb53e80836ff1e185d3ccd7782ea846c2e91a7b0808986666e0bdadbfb7bdd65670a589a4d2478e9adcafe97c6ee23614bcb2ecc23580f4d2e3cc1ecfec25c50da4bc754dde6c8bfd8d1fc16956c74d8e9196046a01dc9f3024e11461c294f29d7421140732fedacac97b8fe50999117d27943c953f18c4ff4f8c258d839764078d4b6ef6e8591e0ff5563b31a39e6374d0d41c8c46921c25e5904a817ef8e39e5c9b71225a83269693e0b7e3218fc5e5a1e8412ba16e588b3d6ac536dce39fcdfce81eec79979ea6872793

m = gmpy2.iroot(c,e)[0]
print(number.long_to_bytes(m))

当然这题，这道题的m很小，我只是对m开了三次根号。

而对于m值很大的情况，循环k，使k*n+c开e次根号，iroot返回的第二个值为True即可

from gmpy2 import iroot
from Crypto.Util import number
n = 0x52d483c27cd806550fbe0e37a61af2e7cf5e0efb723dfc81174c918a27627779b21fa3c851e9e94188eaee3d5cd6f752406a43fbecb53e80836ff1e185d3ccd7782ea846c2e91a7b0808986666e0bdadbfb7bdd65670a589a4d2478e9adcafe97c6ee23614bcb2ecc23580f4d2e3cc1ecfec25c50da4bc754dde6c8bfd8d1fc16956c74d8e9196046a01dc9f3024e11461c294f29d7421140732fedacac97b8fe50999117d27943c953f18c4ff4f8c258d839764078d4b6ef6e8591e0ff5563b31a39e6374d0d41c8c46921c25e5904a817ef8e39e5c9b71225a83269693e0b7e3218fc5e5a1e8412ba16e588b3d6ac536dce39fcdfce81eec79979ea6872793
c = 0x10652cdfaa6b63f6d7bd1109da08181e500e5643f5b240a9024bfa84d5f2cac9310562978347bb232d63e7289283871efab83d84ff5a7b64a94a79d34cfbd4ef121723ba1f663e514f83f6f01492b4e13e1bb4296d96ea5a353d3bf2edd2f449c03c4a3e995237985a596908adc741f32365
e = 0x3
k = 0
while 1:
    res=iroot(c+k*n,e)
    if(res[1]==True):
        print(number.long_to_bytes(res[0]))
        break
    k=k+1

公因数分解n

[BJDCTF2020]RSA（公因数分解n+爆破e）

from Crypto.Util.number import getPrime,bytes_to_long

flag=open("flag","rb").read()

p=getPrime(1024)
q=getPrime(1024)
assert(e<100000)
n=p*q
m=bytes_to_long(flag)
c=pow(m,e,n)
print c,n
print pow(294,e,n)

p=getPrime(1024)
n=p*q
m=bytes_to_long("BJD"*32)
c=pow(m,e,n)
print c,n

'''
output:
12641635617803746150332232646354596292707861480200207537199141183624438303757120570096741248020236666965755798009656547738616399025300123043766255518596149348930444599820675230046423373053051631932557230849083426859490183732303751744004874183062594856870318614289991675980063548316499486908923209627563871554875612702079100567018698992935818206109087568166097392314105717555482926141030505639571708876213167112187962584484065321545727594135175369233925922507794999607323536976824183162923385005669930403448853465141405846835919842908469787547341752365471892495204307644586161393228776042015534147913888338316244169120  13508774104460209743306714034546704137247627344981133461801953479736017021401725818808462898375994767375627749494839671944543822403059978073813122441407612530658168942987820256786583006947001711749230193542370570950705530167921702835627122401475251039000775017381633900222474727396823708695063136246115652622259769634591309421761269548260984426148824641285010730983215377509255011298737827621611158032976420011662547854515610597955628898073569684158225678333474543920326532893446849808112837476684390030976472053905069855522297850688026960701186543428139843783907624317274796926248829543413464754127208843070331063037
381631268825806469518166370387352035475775677163615730759454343913563615970881967332407709901235637718936184198930226303761876517101208677107311006065728014220477966000620964056616058676999878976943319063836649085085377577273214792371548775204594097887078898598463892440141577974544939268247818937936607013100808169758675042264568547764031628431414727922168580998494695800403043312406643527637667466318473669542326169218665366423043579003388486634167642663495896607282155808331902351188500197960905672207046579647052764579411814305689137519860880916467272056778641442758940135016400808740387144508156358067955215018
979153370552535153498477459720877329811204688208387543826122582132404214848454954722487086658061408795223805022202997613522014736983452121073860054851302343517756732701026667062765906277626879215457936330799698812755973057557620930172778859116538571207100424990838508255127616637334499680058645411786925302368790414768248611809358160197554369255458675450109457987698749584630551177577492043403656419968285163536823819817573531356497236154342689914525321673807925458651854768512396355389740863270148775362744448115581639629326362342160548500035000156097215446881251055505465713854173913142040976382500435185442521721  12806210903061368369054309575159360374022344774547459345216907128193957592938071815865954073287532545947370671838372144806539753829484356064919357285623305209600680570975224639214396805124350862772159272362778768036844634760917612708721787320159318432456050806227784435091161119982613987303255995543165395426658059462110056431392517548717447898084915167661172362984251201688639469652283452307712821398857016487590794996544468826705600332208535201443322267298747117528882985955375246424812616478327182399461709978893464093245135530135430007842223389360212803439850867615121148050034887767584693608776323252233254261047
'''

关于e的爆破脚本：

p2 = 381631268825806469518166370387352035475775677163615730759454343913563615970881967332407709901235637718936184198930226303761876517101208677107311006065728014220477966000620964056616058676999878976943319063836649085085377577273214792371548775204594097887078898598463892440141577974544939268247818937936607013100808169758675042264568547764031628431414727922168580998494695800403043312406643527637667466318473669542326169218665366423043579003388486634167642663495896607282155808331902351188500197960905672207046579647052764579411814305689137519860880916467272056778641442758940135016400808740387144508156358067955215018
n2 = 13508774104460209743306714034546704137247627344981133461801953479736017021401725818808462898375994767375627749494839671944543822403059978073813122441407612530658168942987820256786583006947001711749230193542370570950705530167921702835627122401475251039000775017381633900222474727396823708695063136246115652622259769634591309421761269548260984426148824641285010730983215377509255011298737827621611158032976420011662547854515610597955628898073569684158225678333474543920326532893446849808112837476684390030976472053905069855522297850688026960701186543428139843783907624317274796926248829543413464754127208843070331063037
e = 1
while 1:
	if pow(294,e,n2) == p2:
		print(e)
		break
	else:
		print(e)
	e += 1
# e = 52361

其余项打算用z3来解的，但是解不出来……

–更新–

忘了一个最重要的条件:当n1,n2很大的时候，q = gcd(n1,n2)!!!

1
2
3

from gmpy2 import *
q = gcd(n1,n2)
# q = 99855353761764939308265951492116976798674681282941462516956577712943717850048051273358745095906207085170915794187749954588685850452162165059831749303473106541930948723000882713453679904525655327168665295207423257922666721077747911860159181041422993030618385436504858943615630219459262419715816361781062898911

求出q，那接下来就好办了：

from gmpy2 import *
from Crypto.Util.number import *
p2 = 381631268825806469518166370387352035475775677163615730759454343913563615970881967332407709901235637718936184198930226303761876517101208677107311006065728014220477966000620964056616058676999878976943319063836649085085377577273214792371548775204594097887078898598463892440141577974544939268247818937936607013100808169758675042264568547764031628431414727922168580998494695800403043312406643527637667466318473669542326169218665366423043579003388486634167642663495896607282155808331902351188500197960905672207046579647052764579411814305689137519860880916467272056778641442758940135016400808740387144508156358067955215018
c1 = 12641635617803746150332232646354596292707861480200207537199141183624438303757120570096741248020236666965755798009656547738616399025300123043766255518596149348930444599820675230046423373053051631932557230849083426859490183732303751744004874183062594856870318614289991675980063548316499486908923209627563871554875612702079100567018698992935818206109087568166097392314105717555482926141030505639571708876213167112187962584484065321545727594135175369233925922507794999607323536976824183162923385005669930403448853465141405846835919842908469787547341752365471892495204307644586161393228776042015534147913888338316244169120  
n2 = 12806210903061368369054309575159360374022344774547459345216907128193957592938071815865954073287532545947370671838372144806539753829484356064919357285623305209600680570975224639214396805124350862772159272362778768036844634760917612708721787320159318432456050806227784435091161119982613987303255995543165395426658059462110056431392517548717447898084915167661172362984251201688639469652283452307712821398857016487590794996544468826705600332208535201443322267298747117528882985955375246424812616478327182399461709978893464093245135530135430007842223389360212803439850867615121148050034887767584693608776323252233254261047
n1 = 13508774104460209743306714034546704137247627344981133461801953479736017021401725818808462898375994767375627749494839671944543822403059978073813122441407612530658168942987820256786583006947001711749230193542370570950705530167921702835627122401475251039000775017381633900222474727396823708695063136246115652622259769634591309421761269548260984426148824641285010730983215377509255011298737827621611158032976420011662547854515610597955628898073569684158225678333474543920326532893446849808112837476684390030976472053905069855522297850688026960701186543428139843783907624317274796926248829543413464754127208843070331063037
q = 99855353761764939308265951492116976798674681282941462516956577712943717850048051273358745095906207085170915794187749954588685850452162165059831749303473106541930948723000882713453679904525655327168665295207423257922666721077747911860159181041422993030618385436504858943615630219459262419715816361781062898911
p1 = n1//q
e = 52361
d = invert(e,(p1-1)*(q-1))
m = pow(c1,d,n1)
print(long_to_bytes(m))
# BJD{p_is_common_divisor}

RSA5（公因数求解）

本来想用CRT的，但是题目中给出的e很大，不适合用。

只能从给出的20个n中找规律了

1 2	# 若n1,n2不互质 p = gcd(n1，n2)

从20个n中找出有公约数的一对，然后找出对应n的p和q，剩余的就顺水推舟了。

import gmpy2
from Crypto.Util.number import *

n1 = 20474918894051778533305262345601880928088284471121823754049725354072477155873778848055073843345820697886641086842612486541250183965966001591342031562953561793332341641334302847996108417466360688139866505179689516589305636902137210185624650854906780037204412206309949199080005576922775773722438863762117750429327585792093447423980002401200613302943834212820909269713876683465817369158585822294675056978970612202885426436071950214538262921077409076160417436699836138801162621314845608796870206834704116707763169847387223307828908570944984416973019427529790029089766264949078038669523465243837675263858062854739083634207
c1 = 974463908243330865728978769213595400782053398596897741316275722596415018912929508637393850919224969271766388710025195039896961956062895570062146947736340342927974992616678893372744261954172873490878805483241196345881721164078651156067119957816422768524442025688079462656755605982104174001635345874022133045402344010045961111720151990412034477755851802769069309069018738541854130183692204758761427121279982002993939745343695671900015296790637464880337375511536424796890996526681200633086841036320395847725935744757993013352804650575068136129295591306569213300156333650910795946800820067494143364885842896291126137320

n2 = 20918819960648891349438263046954902210959146407860980742165930253781318759285692492511475263234242002509419079545644051755251311392635763412553499744506421566074721268822337321637265942226790343839856182100575539845358877493718334237585821263388181126545189723429262149630651289446553402190531135520836104217160268349688525168375213462570213612845898989694324269410202496871688649978370284661017399056903931840656757330859626183773396574056413017367606446540199973155630466239453637232936904063706551160650295031273385619470740593510267285957905801566362502262757750629162937373721291789527659531499435235261620309759
c2 = 15819636201971185538694880505120469332582151856714070824521803121848292387556864177196229718923770810072104155432038682511434979353089791861087415144087855679134383396897817458726543883093567600325204596156649305930352575274039425470836355002691145864435755333821133969266951545158052745938252574301327696822347115053614052423028835532509220641378760800693351542633860702225772638930501021571415907348128269681224178300248272689705308911282208685459668200507057183420662959113956077584781737983254788703048275698921427029884282557468334399677849962342196140864403989162117738206246183665814938783122909930082802031855

n3 = 25033254625906757272369609119214202033162128625171246436639570615263949157363273213121556825878737923265290579551873824374870957467163989542063489416636713654642486717219231225074115269684119428086352535471683359486248203644461465935500517901513233739152882943010177276545128308412934555830087776128355125932914846459470221102007666912211992310538890654396487111705385730502843589727289829692152177134753098649781412247065660637826282055169991824099110916576856188876975621376606634258927784025787142263367152947108720757222446686415627479703666031871635656314282727051189190889008763055811680040315277078928068816491
c3 = 4185308529416874005831230781014092407198451385955677399668501833902623478395669279404883990725184332709152443372583701076198786635291739356770857286702107156730020004358955622511061410661058982622055199736820808203841446796305284394651714430918690389486920560834672316158146453183789412140939029029324756035358081754426645160033262924330248675216108270980157049705488620263485129480952814764002865280019185127662449318324279383277766416258142275143923532168798413011028271543085249029048997452212503111742302302065401051458066585395360468447460658672952851643547193822775218387853623453638025492389122204507555908862

n4 = 21206968097314131007183427944486801953583151151443627943113736996776787181111063957960698092696800555044199156765677935373149598221184792286812213294617749834607696302116136745662816658117055427803315230042700695125718401646810484873064775005221089174056824724922160855810527236751389605017579545235876864998419873065217294820244730785120525126565815560229001887622837549118168081685183371092395128598125004730268910276024806808565802081366898904032509920453785997056150497645234925528883879419642189109649009132381586673390027614766605038951015853086721168018787523459264932165046816881682774229243688581614306480751
c4 = 4521038011044758441891128468467233088493885750850588985708519911154778090597136126150289041893454126674468141393472662337350361712212694867311622970440707727941113263832357173141775855227973742571088974593476302084111770625764222838366277559560887042948859892138551472680654517814916609279748365580610712259856677740518477086531592233107175470068291903607505799432931989663707477017904611426213770238397005743730386080031955694158466558475599751940245039167629126576784024482348452868313417471542956778285567779435940267140679906686531862467627238401003459101637191297209422470388121802536569761414457618258343550613

n5 = 22822039733049388110936778173014765663663303811791283234361230649775805923902173438553927805407463106104699773994158375704033093471761387799852168337898526980521753614307899669015931387819927421875316304591521901592823814417756447695701045846773508629371397013053684553042185725059996791532391626429712416994990889693732805181947970071429309599614973772736556299404246424791660679253884940021728846906344198854779191951739719342908761330661910477119933428550774242910420952496929605686154799487839923424336353747442153571678064520763149793294360787821751703543288696726923909670396821551053048035619499706391118145067
c5 = 15406498580761780108625891878008526815145372096234083936681442225155097299264808624358826686906535594853622687379268969468433072388149786607395396424104318820879443743112358706546753935215756078345959375299650718555759698887852318017597503074317356745122514481807843745626429797861463012940172797612589031686718185390345389295851075279278516147076602270178540690147808314172798987497259330037810328523464851895621851859027823681655934104713689539848047163088666896473665500158179046196538210778897730209572708430067658411755959866033531700460551556380993982706171848970460224304996455600503982223448904878212849412357

n6 = 21574139855341432908474064784318462018475296809327285532337706940126942575349507668289214078026102682252713757703081553093108823214063791518482289846780197329821139507974763780260290309600884920811959842925540583967085670848765317877441480914852329276375776405689784571404635852204097622600656222714808541872252335877037561388406257181715278766652824786376262249274960467193961956690974853679795249158751078422296580367506219719738762159965958877806187461070689071290948181949561254144310776943334859775121650186245846031720507944987838489723127897223416802436021278671237227993686791944711422345000479751187704426369
c6 = 20366856150710305124583065375297661819795242238376485264951185336996083744604593418983336285185491197426018595031444652123288461491879021096028203694136683203441692987069563513026001861435722117985559909692670907347563594578265880806540396777223906955491026286843168637367593400342814725694366078337030937104035993569672959361347287894143027186846856772983058328919716702982222142848848117768499996617588305301483085428547267337070998767412540225911508196842253134355901263861121500650240296746702967594224401650220168780537141654489215019142122284308116284129004257364769474080721001708734051264841350424152506027932

n7 = 25360227412666612490102161131174584819240931803196448481224305250583841439581008528535930814167338381983764991296575637231916547647970573758269411168219302370541684789125112505021148506809643081950237623703181025696585998044695691322012183660424636496897073045557400768745943787342548267386564625462143150176113656264450210023925571945961405709276631990731602198104287528528055650050486159837612279600415259486306154947514005408907590083747758953115486124865486720633820559135063440942528031402951958557630833503775112010715604278114325528993771081233535247118481765852273252404963430792898948219539473312462979849137
c7 = 19892772524651452341027595619482734356243435671592398172680379981502759695784087900669089919987705675899945658648623800090272599154590123082189645021800958076861518397325439521139995652026377132368232502108620033400051346127757698623886142621793423225749240286511666556091787851683978017506983310073524398287279737680091787333547538239920607761080988243639547570818363788673249582783015475682109984715293163137324439862838574460108793714172603672477766831356411304446881998674779501188163600664488032943639694828698984739492200699684462748922883550002652913518229322945040819064133350314536378694523704793396169065179

n8 = 22726855244632356029159691753451822163331519237547639938779517751496498713174588935566576167329576494790219360727877166074136496129927296296996970048082870488804456564986667129388136556137013346228118981936899510687589585286517151323048293150257036847475424044378109168179412287889340596394755257704938006162677656581509375471102546261355748251869048003600520034656264521931808651038524134185732929570384705918563982065684145766427962502261522481994191989820110575981906998431553107525542001187655703534683231777988419268338249547641335718393312295800044734534761692799403469497954062897856299031257454735945867491191
c8 = 6040119795175856407541082360023532204614723858688636724822712717572759793960246341800308149739809871234313049629732934797569781053000686185666374833978403290525072598774001731350244744590772795701065129561898116576499984185920661271123665356132719193665474235596884239108030605882777868856122378222681140570519180321286976947154042272622411303981011302586225630859892731724640574658125478287115198406253847367979883768000812605395482952698689604477719478947595442185921480652637868335673233200662100621025061500895729605305665864693122952557361871523165300206070325660353095592778037767395360329231331322823610060006

n9 = 23297333791443053297363000786835336095252290818461950054542658327484507406594632785712767459958917943095522594228205423428207345128899745800927319147257669773812669542782839237744305180098276578841929496345963997512244219376701787616046235397139381894837435562662591060768476997333538748065294033141610502252325292801816812268934171361934399951548627267791401089703937389012586581080223313060159456238857080740699528666411303029934807011214953984169785844714159627792016926490955282697877141614638806397689306795328344778478692084754216753425842557818899467945102646776342655167655384224860504086083147841252232760941
c9 = 5418120301208378713115889465579964257871814114515046096090960159737859076829258516920361577853903925954198406843757303687557848302302200229295916902430205737843601806700738234756698575708612424928480440868739120075888681672062206529156566421276611107802917418993625029690627196813830326369874249777619239603300605876865967515719079797115910578653562787899019310139945904958024882417833736304894765433489476234575356755275147256577387022873348906900149634940747104513850154118106991137072643308620284663108283052245750945228995387803432128842152251549292698947407663643895853432650029352092018372834457054271102816934

n10 = 28873667904715682722987234293493200306976947898711255064125115933666968678742598858722431426218914462903521596341771131695619382266194233561677824357379805303885993804266436810606263022097900266975250431575654686915049693091467864820512767070713267708993899899011156106766178906700336111712803362113039613548672937053397875663144794018087017731949087794894903737682383916173267421403408140967713071026001874733487295007501068871044649170615709891451856792232315526696220161842742664778581287321318748202431466508948902745314372299799561625186955234673012098210919745879882268512656931714326782335211089576897310591491
c10 = 9919880463786836684987957979091527477471444996392375244075527841865509160181666543016317634963512437510324198702416322841377489417029572388474450075801462996825244657530286107428186354172836716502817609070590929769261932324275353289939302536440310628698349244872064005700644520223727670950787924296004296883032978941200883362653993351638545860207179022472492671256630427228461852668118035317021428675954874947015197745916918197725121122236369382741533983023462255913924692806249387449016629865823316402366017657844166919846683497851842388058283856219900535567427103603869955066193425501385255322097901531402103883869

n11 = 22324685947539653722499932469409607533065419157347813961958075689047690465266404384199483683908594787312445528159635527833904475801890381455653807265501217328757871352731293000303438205315816792663917579066674842307743845261771032363928568844669895768092515658328756229245837025261744260614860746997931503548788509983868038349720225305730985576293675269073709022350700836510054067641753713212999954307022524495885583361707378513742162566339010134354907863733205921845038918224463903789841881400814074587261720283879760122070901466517118265422863420376921536734845502100251460872499122236686832189549698020737176683019
c11 = 1491527050203294989882829248560395184804977277747126143103957219164624187528441047837351263580440686474767380464005540264627910126483129930668344095814547592115061057843470131498075060420395111008619027199037019925701236660166563068245683975787762804359520164701691690916482591026138582705558246869496162759780878437137960823000043988227303003876410503121370163303711603359430764539337597866862508451528158285103251810058741879687875218384160282506172706613359477657215420734816049393339593755489218588796607060261897905233453268671411610631047340459487937479511933450369462213795738933019001471803157607791738538467

n12 = 27646746423759020111007828653264027999257847645666129907789026054594393648800236117046769112762641778865620892443423100189619327585811384883515424918752749559627553637785037359639801125213256163008431942593727931931898199727552768626775618479833029101249692573716030706695702510982283555740851047022672485743432464647772882314215176114732257497240284164016914018689044557218920300262234652840632406067273375269301008409860193180822366735877288205783314326102263756503786736122321348320031950012144905869556204017430593656052867939493633163499580242224763404338807022510136217187779084917996171602737036564991036724299
c12 = 21991524128957260536043771284854920393105808126700128222125856775506885721971193109361315961129190814674647136464887087893990660894961612838205086401018885457667488911898654270235561980111174603323721280911197488286585269356849579263043456316319476495888696219344219866516861187654180509247881251251278919346267129904739277386289240394384575124331135655943513831009934023397457082184699737734388823763306805326430395849935770213817533387235486307008892410920611669932693018165569417445885810825749609388627231235840912644654685819620931663346297596334834498661789016450371769203650109994771872404185770230172934013971

n13 = 20545487405816928731738988374475012686827933709789784391855706835136270270933401203019329136937650878386117187776530639342572123237188053978622697282521473917978282830432161153221216194169879669541998840691383025487220850872075436064308499924958517979727954402965612196081404341651517326364041519250125036424822634354268773895465698920883439222996581226358595873993976604699830613932320720554130011671297944433515047180565484495191003887599891289037982010216357831078328159028953222056918189365840711588671093333013117454034313622855082795813122338562446223041211192277089225078324682108033843023903550172891959673551
c13 = 14227439188191029461250476692790539654619199888487319429114414557975376308688908028140817157205579804059783807641305577385724758530138514972962209062230576107406142402603484375626077345190883094097636019771377866339531511965136650567412363889183159616188449263752475328663245311059988337996047359263288837436305588848044572937759424466586870280512424336807064729894515840552404756879590698797046333336445465120445087587621743906624279621779634772378802959109714400516183718323267273824736540168545946444437586299214110424738159957388350785999348535171553569373088251552712391288365295267665691357719616011613628772175

n14 = 27359727711584277234897157724055852794019216845229798938655814269460046384353568138598567755392559653460949444557879120040796798142218939251844762461270251672399546774067275348291003962551964648742053215424620256999345448398805278592777049668281558312871773979931343097806878701114056030041506690476954254006592555275342579529625231194321357904668512121539514880704046969974898412095675082585315458267591016734924646294357666924293908418345508902112711075232047998775303603175363964055048589769318562104883659754974955561725694779754279606726358588862479198815999276839234952142017210593887371950645418417355912567987
c14 = 3788529784248255027081674540877016372807848222776887920453488878247137930578296797437647922494510483767651150492933356093288965943741570268943861987024276610712717409139946409513963043114463933146088430004237747163422802959250296602570649363016151581364006795894226599584708072582696996740518887606785460775851029814280359385763091078902301957226484620428513604630585131511167015763190591225884202772840456563643159507805711004113901417503751181050823638207803533111429510911616160851391754754434764819568054850823810901159821297849790005646102129354035735350124476838786661542089045509656910348676742844957008857457

n15 = 27545937603751737248785220891735796468973329738076209144079921449967292572349424539010502287564030116831261268197384650511043068738911429169730640135947800885987171539267214611907687570587001933829208655100828045651391618089603288456570334500533178695238407684702251252671579371018651675054368606282524673369983034682330578308769886456335818733827237294570476853673552685361689144261552895758266522393004116017849397346259119221063821663280935820440671825601452417487330105280889520007917979115568067161590058277418371493228631232457972494285014767469893647892888681433965857496916110704944758070268626897045014782837
c15 = 14069112970608895732417039977542732665796601893762401500878786871680645798754783315693511261740059725171342404186571066972546332813667711135661176659424619936101038903439144294886379322591635766682645179888058617577572409307484708171144488708410543462972008179994594087473935638026612679389759756811490524127195628741262871304427908481214992471182859308828778119005750928935764927967212343526503410515793717201360360437981322576798056276657140363332700714732224848346808963992302409037706094588964170239521193589470070839790404597252990818583717869140229811712295005710540476356743378906642267045723633874011649259842

n16 = 25746162075697911560263181791216433062574178572424600336856278176112733054431463253903433128232709054141607100891177804285813783247735063753406524678030561284491481221681954564804141454666928657549670266775659862814924386584148785453647316864935942772919140563506305666207816897601862713092809234429096584753263707828899780979223118181009293655563146526792388913462557306433664296966331469906428665127438829399703002867800269947855869262036714256550075520193125987011945192273531732276641728008406855871598678936585324782438668746810516660152018244253008092470066555687277138937298747951929576231036251316270602513451
c16 = 17344284860275489477491525819922855326792275128719709401292545608122859829827462088390044612234967551682879954301458425842831995513832410355328065562098763660326163262033200347338773439095709944202252494552172589503915965931524326523663289777583152664722241920800537867331030623906674081852296232306336271542832728410803631170229642717524942332390842467035143631504401140727083270732464237443915263865880580308776111219718961746378842924644142127243573824972533819479079381023103585862099063382129757560124074676150622288706094110075567706403442920696472627797607697962873026112240527498308535903232663939028587036724

n17 = 23288486934117120315036919418588136227028485494137930196323715336208849327833965693894670567217971727921243839129969128783853015760155446770590696037582684845937132790047363216362087277861336964760890214059732779383020349204803205725870225429985939570141508220041286857810048164696707018663758416807708910671477407366098883430811861933014973409390179948577712579749352299440310543689035651465399867908428885541237776143404376333442949397063249223702355051571790555151203866821867908531733788784978667478707672984539512431549558672467752712004519300318999208102076732501412589104904734983789895358753664077486894529499
c17 = 10738254418114076548071448844964046468141621740603214384986354189105236977071001429271560636428075970459890958274941762528116445171161040040833357876134689749846940052619392750394683504816081193432350669452446113285638982551762586656329109007214019944975816434827768882704630460001209452239162896576191876324662333153835533956600295255158377025198426950944040643235430211011063586032467724329735785947372051759042138171054165854842472990583800899984893232549092766400510300083585513014171220423103452292891496141806956300396540682381668367564569427813092064053993103537635994311143010708814851867239706492577203899024

n18 = 19591441383958529435598729113936346657001352578357909347657257239777540424811749817783061233235817916560689138344041497732749011519736303038986277394036718790971374656832741054547056417771501234494768509780369075443550907847298246275717420562375114406055733620258777905222169702036494045086017381084272496162770259955811174440490126514747876661317750649488774992348005044389081101686016446219264069971370646319546429782904810063020324704138495608761532563310699753322444871060383693044481932265801505819646998535192083036872551683405766123968487907648980900712118052346174533513978009131757167547595857552370586353973
c18 = 3834917098887202931981968704659119341624432294759361919553937551053499607440333234018189141970246302299385742548278589896033282894981200353270637127213483172182529890495903425649116755901631101665876301799865612717750360089085179142750664603454193642053016384714515855868368723508922271767190285521137785688075622832924829248362774476456232826885801046969384519549385428259591566716890844604696258783639390854153039329480726205147199247183621535172450825979047132495439603840806501254997167051142427157381799890725323765558803808030109468048682252028720241357478614704610089120810367192414352034177484688502364022887

n19 = 19254242571588430171308191757871261075358521158624745702744057556054652332495961196795369630484782930292003238730267396462491733557715379956969694238267908985251699834707734400775311452868924330866502429576951934279223234676654749272932769107390976321208605516299532560054081301829440688796904635446986081691156842271268059970762004259219036753174909942343204432795076377432107630203621754552804124408792358220071862369443201584155711893388877350138023238624566616551246804054720492816226651467017802504094070614892556444425915920269485861799532473383304622064493223627552558344088839860178294589481899206318863310603
c19 = 6790553533991297205804561991225493105312398825187682250780197510784765226429663284220400480563039341938599783346724051076211265663468643826430109013245014035811178295081939958687087477312867720289964506097819762095244479129359998867671811819738196687884696680463458661374310994610760009474264115750204920875527434486437536623589684519411519100170291423367424938566820315486507444202022408003879118465761273916755290898112991525546114191064022991329724370064632569903856189236177894007766690782630247443895358893983735822824243487181851098787271270256780891094405121947631088729917398317652320497765101790132679171889

n20 = 26809700251171279102974962949184411136459372267620535198421449833298448092580497485301953796619185339316064387798092220298630428207556482805739803420279056191194360049651767412572609187680508073074653291350998253938793269214230457117194434853888765303403385824786231859450351212449404870776320297419712486574804794325602760347306432927281716160368830187944940128907971027838510079519466846176106565164730963988892400240063089397720414921398936399927948235195085202171264728816184532651138221862240969655185596628285814057082448321749567943946273776184657698104465062749244327092588237927996419620170254423837876806659
c20 = 386213556608434013769864727123879412041991271528990528548507451210692618986652870424632219424601677524265011043146748309774067894985069288067952546139416819404039688454756044862784630882833496090822568580572859029800646671301748901528132153712913301179254879877441322285914544974519727307311002330350534857867516466612474769753577858660075830592891403551867246057397839688329172530177187042229028685862036140779065771061933528137423019407311473581832405899089709251747002788032002094495379614686544672969073249309703482556386024622814731015767810042969813752548617464974915714425595351940266077021672409858645427346

cList = [c1,c2,c3,c4,c5,c6,c7,c8,c9,c10,c11,c12,c13,c14,c15,c16,c17,c18,c19,c20]
nList = [n1,n2,n3,n4,n5,n6,n7,n8,n9,n10,n11,n12,n13,n14,n15,n16,n17,n18,n19,n20]

e = 65537

for i in range(len(nList)):
	for j in range(len(nList)):
		if i!= j:
			if gmpy2.gcd(nList[i],nList[j]) != 1:
				print(i,j)
				print(gmpy2.gcd(nList[i],nList[j]))

# 4 17
# 132585806383798600305426957307612567604223562626764190211333136246643723811046149337852966828729052476725552361132437370521548707664977123165279305052971868012755509160408641100548744046621516877981864180076497524093201404558036301820216274968638825245150755772559259575544101918590311068466601618472464832499
q = 132585806383798600305426957307612567604223562626764190211333136246643723811046149337852966828729052476725552361132437370521548707664977123165279305052971868012755509160408641100548744046621516877981864180076497524093201404558036301820216274968638825245150755772559259575544101918590311068466601618472464832499
p = nList[4]//q
d = gmpy2.invert(e,(p-1)*(q-1))
m = pow(cList[4],d,nList[4])
print(long_to_bytes(m))
# flag{abdcbe5fd94e23b3de429223ab9c2fdf}

[脚本参考](https://blog.csdn.net/weixin_44017838/article/details/104878645?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522164958629416780261970846%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=164958629416780261970846&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduend~default-2-104878645.142 ** v7 ** pc_search_result_control_group,157 ** v4 ** control&utm_term=RSA5&spm=1018.2226.3001.4187)

低加密指数广播攻击(中国剩余定理)

RSA4 (中国剩余定理+低加密指数攻击)

来复习一下加密和解密的规则

1 2	c = m e % n m = c d % n

题目给了三个N和三个C，考虑用中国剩余定律（CRT）求出m ** e。

这题给出的数据仔细观察，可以知道是五进制数据，所以还需要转化，int(x,5)即可

题目中还没有给出e，这种题目中e通常都很小，低指数加密，只需要遍历求出的m ** e，开对应的根号即可。

import gmpy2
from Crypto.Util.number import *

#利用中国剩余定理求解同余方程，aList：余数，mList：模数
def CRT(aList, mList):
    M = 1
    for i in mList:
        M = M * i   #计算M = ∏ mi
    #print(M)
    x = 0
    for i in range(len(mList)):
        Mi = M // mList[i]   #计算Mi
        Mi_inverse = gmpy2.invert(Mi, mList[i]) #计算Mi的逆元
        x += aList[i] * Mi * Mi_inverse #构造x各项
    x = x % M
    return x

if __name__ == "__main__":
    #========== n c ==========
    n1 = "331310324212000030020214312244232222400142410423413104441140203003243002104333214202031202212403400220031202142322434104143104244241214204444443323000244130122022422310201104411044030113302323014101331214303223312402430402404413033243132101010422240133122211400434023222214231402403403200012221023341333340042343122302113410210110221233241303024431330001303404020104442443120130000334110042432010203401440404010003442001223042211442001413004"
    c1 = "310020004234033304244200421414413320341301002123030311202340222410301423440312412440240244110200112141140201224032402232131204213012303204422003300004011434102141321223311243242010014140422411342304322201241112402132203101131221223004022003120002110230023341143201404311340311134230140231412201333333142402423134333211302102413111111424430032440123340034044314223400401224111323000242234420441240411021023100222003123214343030122032301042243"
    n2 = "302240000040421410144422133334143140011011044322223144412002220243001141141114123223331331304421113021231204322233120121444434210041232214144413244434424302311222143224402302432102242132244032010020113224011121043232143221203424243134044314022212024343100042342002432331144300214212414033414120004344211330224020301223033334324244031204240122301242232011303211220044222411134403012132420311110302442344021122101224411230002203344140143044114"
    c2 = "112200203404013430330214124004404423210041321043000303233141423344144222343401042200334033203124030011440014210112103234440312134032123400444344144233020130110134042102220302002413321102022414130443041144240310121020100310104334204234412411424420321211112232031121330310333414423433343322024400121200333330432223421433344122023012440013041401423202210124024431040013414313121123433424113113414422043330422002314144111134142044333404112240344"
    n3 = "332200324410041111434222123043121331442103233332422341041340412034230003314420311333101344231212130200312041044324431141033004333110021013020140020011222012300020041342040004002220210223122111314112124333211132230332124022423141214031303144444134403024420111423244424030030003340213032121303213343020401304243330001314023030121034113334404440421242240113103203013341231330004332040302440011324004130324034323430143102401440130242321424020323"
    c3 = "10013444120141130322433204124002242224332334011124210012440241402342100410331131441303242011002101323040403311120421304422222200324402244243322422444414043342130111111330022213203030324422101133032212042042243101434342203204121042113212104212423330331134311311114143200011240002111312122234340003403312040401043021433112031334324322123304112340014030132021432101130211241134422413442312013042141212003102211300321404043012124332013240431242"
    
    cList = [int(c1,5), int(c2,5), int(c3,5)]
    nList = [int(n1,5), int(n2,5), int(n3,5)]
    m_e = CRT(cList, nList) #计算m ** e
    for e in range(1, 10):  #遍历e求解
        m, f = gmpy2.iroot(m_e, e) #m_e开e次根
        print("加密指数e = %d："%e)
        flag = long_to_bytes(m)
        print(flag)
# noxCTF{D4mn_y0u_h4s74d_wh47_4_b100dy_b4s74rd!}

代码来源

rsa-wiener-attack

rsa2

方法一：在线分解


N = 101991809777553253470276751399264740131157682329252673501792154507006158434432009141995367241962525705950046253400188884658262496534706438791515071885860897552736656899566915731297225817250639873643376310103992170646906557242832893914902053581087502512787303322747780420210884852166586717636559058152544979471
e = 46731919563265721307105180410302518676676135509737992912625092976849075262192092549323082367518264378630543338219025744820916471913696072050291990620486581719410354385121760761374229374847695148230596005409978383369740305816082770283909611956355972181848077519920922059268376958811713365106925235218265173085

import hashlib
flag = "flag{" + hashlib.md5(hex(d)).hexdigest() + "}"

在线网站分解出p和q

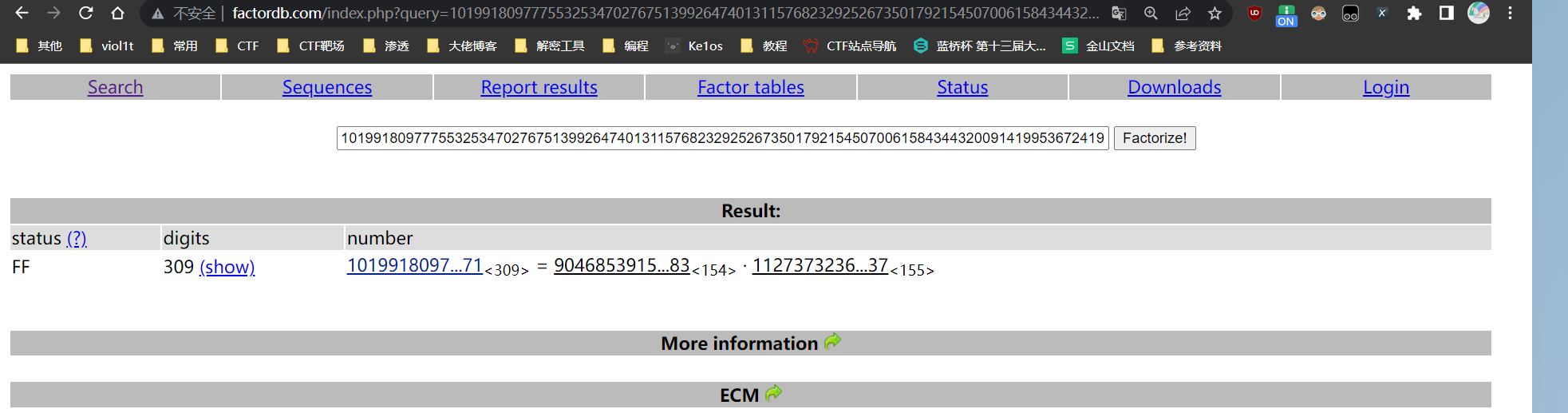
脚本：

import gmpy2
p = 9046853915223503351787031888977627106934564043204783593118678181991596316582877057556463152579621699010610569526573031954779520781448550677767565207407183

q = 11273732364123571293429600400343309403733952146912318879993851141423284675797325272321856863528776914709992821287788339848962916204774010644058033316303937

d = gmpy2.invert(e,(p-1)*(q-1))
flag = "flag{" + hashlib.md5(hex(d)).hexdigest() + "}"
print(flag)

注意该脚本需要在python2环境中跑出来，如果在python3中，则会提醒需要编码，而且结果不一致……

方法二：rsa-wiener-attack

当e非常大，和n差不多大的时候，就能考虑使用wiener-attack脚本来解题了。

使用的脚本https://github.com/pablocelayes/rsa-wiener-attack

需要将脚本放在rsa-wiener-attack-master的目录下。

from Crypto.Util.number import *
from Crypto.PublicKey import RSA
import ContinuedFractions, Arithmetic
import gmpy2
import hashlib


e = 46731919563265721307105180410302518676676135509737992912625092976849075262192092549323082367518264378630543338219025744820916471913696072050291990620486581719410354385121760761374229374847695148230596005409978383369740305816082770283909611956355972181848077519920922059268376958811713365106925235218265173085


n = 101991809777553253470276751399264740131157682329252673501792154507006158434432009141995367241962525705950046253400188884658262496534706438791515071885860897552736656899566915731297225817250639873643376310103992170646906557242832893914902053581087502512787303322747780420210884852166586717636559058152544979471


def wiener_hack(e, n):
    frac = ContinuedFractions.rational_to_contfrac(e, n)
    convergents = ContinuedFractions.convergents_from_contfrac(frac)
    for (k, d) in convergents:
        if k != 0 and (e * d - 1) % k == 0:
            phi = (e * d - 1) // k
            s = n - phi + 1
            discr = s * s - 4 * n
            if (discr >= 0):
                t = Arithmetic.is_perfect_square(discr)
                if t != -1 and (s + t) % 2 == 0:
                    print("Hacked!")
                    return d
    return False
d = wiener_hack(e, n)
print(d)
print(hex(d))
flag = "flag{" + hashlib.md5(hex(d)).hexdigest() + "}"
print(flag)

注意该脚本也需要在python2环境中跑

数学推理

[BJDCTF2020]easyrsa （反三角函数求导）

from Crypto.Util.number import getPrime,bytes_to_long
from sympy import Derivative
from fractions import Fraction
from secret import flag

p=getPrime(1024)
q=getPrime(1024)
e=65537
n=p*q
z=Fraction(1,Derivative(arctan(p),p)) - Fraction(1,Derivative(arth(q),q))
m=bytes_to_long(flag)
c=pow(m,e,n)
print(c,z,n)
'''
output:
7922547866857761459807491502654216283012776177789511549350672958101810281348402284098310147796549430689253803510994877420135537268549410652654479620858691324110367182025648788407041599943091386227543182157746202947099572389676084392706406084307657000104665696654409155006313203957292885743791715198781974205578654792123191584957665293208390453748369182333152809882312453359706147808198922916762773721726681588977103877454119043744889164529383188077499194932909643918696646876907327364751380953182517883134591810800848971719184808713694342985458103006676013451912221080252735948993692674899399826084848622145815461035
32115748677623209667471622872185275070257924766015020072805267359839059393284316595882933372289732127274076434587519333300142473010344694803885168557548801202495933226215437763329280242113556524498457559562872900811602056944423967403777623306961880757613246328729616643032628964072931272085866928045973799374711846825157781056965164178505232524245809179235607571567174228822561697888645968559343608375331988097157145264357626738141646556353500994924115875748198318036296898604097000938272195903056733565880150540275369239637793975923329598716003350308259321436752579291000355560431542229699759955141152914708362494482
15310745161336895413406690009324766200789179248896951942047235448901612351128459309145825547569298479821101249094161867207686537607047447968708758990950136380924747359052570549594098569970632854351825950729752563502284849263730127586382522703959893392329333760927637353052250274195821469023401443841395096410231843592101426591882573405934188675124326997277775238287928403743324297705151732524641213516306585297722190780088180705070359469719869343939106529204798285957516860774384001892777525916167743272419958572055332232056095979448155082465977781482598371994798871917514767508394730447974770329967681767625495394441

'''

其中Fraction()是分数，Fraction(1,x)就是求倒数

Derivative(f(x),x)是求f(x)关于x的导数

反正切函数arctanx的求导公式：1 /（ 1 + x^2 ）

反双曲正切 arthx的求导公式：1 /（1 - x^2 )

所以 z = p ^ 2 + q ^ 2

因为p*q = n，所以我们通过z3来求解p和q

from z3 import *

z = 32115748677623209667471622872185275070257924766015020072805267359839059393284316595882933372289732127274076434587519333300142473010344694803885168557548801202495933226215437763329280242113556524498457559562872900811602056944423967403777623306961880757613246328729616643032628964072931272085866928045973799374711846825157781056965164178505232524245809179235607571567174228822561697888645968559343608375331988097157145264357626738141646556353500994924115875748198318036296898604097000938272195903056733565880150540275369239637793975923329598716003350308259321436752579291000355560431542229699759955141152914708362494482
n = 15310745161336895413406690009324766200789179248896951942047235448901612351128459309145825547569298479821101249094161867207686537607047447968708758990950136380924747359052570549594098569970632854351825950729752563502284849263730127586382522703959893392329333760927637353052250274195821469023401443841395096410231843592101426591882573405934188675124326997277775238287928403743324297705151732524641213516306585297722190780088180705070359469719869343939106529204798285957516860774384001892777525916167743272419958572055332232056095979448155082465977781482598371994798871917514767508394730447974770329967681767625495394441

x = Solver()
p,q = Ints("p q")
x.add(p*q == n)
x.add(p**2 + q**2 == z)
x.check()
print(x.model())
# p = 144564833334456076455156647979862690498796694770100520405218930055633597500009574663803955456004439398699669751249623406199542605271188909145969364476344963078599240058180033000440459281558347909876143313940657252737586803051935392596519226965519859474501391969755712097119163926672753588797180811711004203301
# q = 105909195259921349656664570904199242969110902804477734660927330311460997899731622163728968380757294196277263615386525795293086103142131020215128282050307177125962302515483190468569376643751587606016315185736245896434947691528567696271911398179288329609207435393579332931583829355558784305002360873458907029141

然后就顺水推舟了

import gmpy2
from Crypto.Util.number import *
p = 144564833334456076455156647979862690498796694770100520405218930055633597500009574663803955456004439398699669751249623406199542605271188909145969364476344963078599240058180033000440459281558347909876143313940657252737586803051935392596519226965519859474501391969755712097119163926672753588797180811711004203301
q = 105909195259921349656664570904199242969110902804477734660927330311460997899731622163728968380757294196277263615386525795293086103142131020215128282050307177125962302515483190468569376643751587606016315185736245896434947691528567696271911398179288329609207435393579332931583829355558784305002360873458907029141
c = 7922547866857761459807491502654216283012776177789511549350672958101810281348402284098310147796549430689253803510994877420135537268549410652654479620858691324110367182025648788407041599943091386227543182157746202947099572389676084392706406084307657000104665696654409155006313203957292885743791715198781974205578654792123191584957665293208390453748369182333152809882312453359706147808198922916762773721726681588977103877454119043744889164529383188077499194932909643918696646876907327364751380953182517883134591810800848971719184808713694342985458103006676013451912221080252735948993692674899399826084848622145815461035
e = 65537
n = p * q
d = gmpy2.invert(e, (q-1)*(p-1))
m = pow(c,d,n)
print(long_to_bytes(m))
# BJD{Advanced_mathematics_is_too_hard!!!}

[RoarCTF2019]RSA （推导+爆破e）

A=(((y%x)**5)%(x%y))**2019+y**316+(y+1)/x
p=next_prime(z*x*y)
q=next_prime(z)
A =  2683349182678714524247469512793476009861014781004924905484127480308161377768192868061561886577048646432382128960881487463427414176114486885830693959404989743229103516924432512724195654425703453612710310587164417035878308390676612592848750287387318129424195208623440294647817367740878211949147526287091298307480502897462279102572556822231669438279317474828479089719046386411971105448723910594710418093977044179949800373224354729179833393219827789389078869290217569511230868967647963089430594258815146362187250855166897553056073744582946148472068334167445499314471518357535261186318756327890016183228412253724
n =  117930806043507374325982291823027285148807239117987369609583515353889814856088099671454394340816761242974462268435911765045576377767711593100416932019831889059333166946263184861287975722954992219766493089630810876984781113645362450398009234556085330943125568377741065242183073882558834603430862598066786475299918395341014877416901185392905676043795425126968745185649565106322336954427505104906770493155723995382318346714944184577894150229037758434597242564815299174950147754426950251419204917376517360505024549691723683358170823416757973059354784142601436519500811159036795034676360028928301979780528294114933347127
c =  41971850275428383625653350824107291609587853887037624239544762751558838294718672159979929266922528917912189124713273673948051464226519605803745171340724343705832198554680196798623263806617998072496026019940476324971696928551159371970207365741517064295956376809297272541800647747885170905737868568000101029143923792003486793278197051326716680212726111099439262589341050943913401067673851885114314709706016622157285023272496793595281054074260451116213815934843317894898883215362289599366101018081513215120728297131352439066930452281829446586562062242527329672575620261776042653626411730955819001674118193293313612128

这题首先是需要求出x和y的值，通过计算可以列出以下的等式

import gmpy2
y = gmpy2.iroot(A,316)[0]
x = (y+1) // (A - y**316 - 1)
# y = 83
# x = 2

p和q是通过x,y,z生成的，可以确定的是，p约是q的166倍，这样我们大概可以求出z的范围，进而可以通过爆破，确定q的值，

z = gmpy2.iroot(n//166,2)[0]

for i in range(2,100000):
    p = z+i
	if n % p == 0:
		print(i,p)
		break
# i = 546 p = 842868045681390934539739959201847552284980179958879667933078453950968566151662147267006293571765463137270594151138695778986165111380428806545593588078365331313084230014618714412959584843421586674162688321942889369912392031882620994944241987153078156389470370195514285850736541078623854327959382156753458569

题目中没有给出我们e值，我们选择爆破e

q = 842868045681390934539739959201847552284980179958879667933078453950968566151662147267006293571765463137270594151138695778986165111380428806545593588078365331313084230014618714412959584843421586674162688321942889369912392031882620994944241987153078156389470370195514285850736541078623854327959382156753458569

p = n//q
phi = (p-1)*(q-1)
for e in range(2,100000):
	if gmpy2.gcd(e,phi) != 1: #e的值，需要与phi满足互质的关系
		continue
	d = gmpy2.invert(e,phi)
	m = pow(c,d,n)
	flag = str(long_to_bytes(m))
	if "CTF" in flag or "flag" in str(flag):
		print(e,flag)
		break
# 65537 b'RoarCTF{wm-l1l1ll1l1l1l111ll}'

这题看似简单，其实很头疼，如何通过给出的A，推断出x,y，再推断出z的范围，小范围爆破出q，最后还需要爆破e，花的时间挺久的……

当然，我尝试了一下在线分解，成功了。但是我认为，比赛中一般不会给出可以轻易分解的n，所以需要锻炼自己数学推理的能力。

过程中自己还编写了一个isPrime函数，和next_prime(n)函数来测试，贴在这边备用（当然使用sympy.nextprime()函数更佳）

import gmpy2
import math

prime = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541]
def isPrime(n): 
	for pri in prime:
		if n == pri:
			continue
		if n % pri == 0:
			return False
	return True

def next_prime(n):
	i = 1
	while True:
		if isPrime(n+i):
			return n+i
			break
		i += 1

[RoarCTF2019]babyRSA (威尔逊定理)

import sympy
import random

def myGetPrime():
    A= getPrime(513)
    print(A)
    B=A-random.randint(1e3,1e5)
    print(B)
    return sympy.nextPrime((B!)%A)
p=myGetPrime()
#A1=21856963452461630437348278434191434000066076750419027493852463513469865262064340836613831066602300959772632397773487317560339056658299954464169264467234407
#B1=21856963452461630437348278434191434000066076750419027493852463513469865262064340836613831066602300959772632397773487317560339056658299954464169264467140596

q=myGetPrime()
#A2=16466113115839228119767887899308820025749260933863446888224167169857612178664139545726340867406790754560227516013796269941438076818194617030304851858418927
#B2=16466113115839228119767887899308820025749260933863446888224167169857612178664139545726340867406790754560227516013796269941438076818194617030304851858351026

r=myGetPrime()

n=p*q*r
#n=85492663786275292159831603391083876175149354309327673008716627650718160585639723100793347534649628330416631255660901307533909900431413447524262332232659153047067908693481947121069070451562822417357656432171870951184673132554213690123308042697361969986360375060954702920656364144154145812838558365334172935931441424096270206140691814662318562696925767991937369782627908408239087358033165410020690152067715711112732252038588432896758405898709010342467882264362733
c=pow(flag,e,n)
#e=0x1001
#c=75700883021669577739329316795450706204502635802310731477156998834710820770245219468703245302009998932067080383977560299708060476222089630209972629755965140317526034680452483360917378812244365884527186056341888615564335560765053550155758362271622330017433403027261127561225585912484777829588501213961110690451987625502701331485141639684356427316905122995759825241133872734362716041819819948645662803292418802204430874521342108413623635150475963121220095236776428
#so,what is the flag?

513位数字的阶乘？蒙了，看大佬的博客才知道原来使用的是威尔逊定律，强到窒息……

简单阐述一下威尔逊定律，就是对于素数n来说，(n - 1)!%n = -1 (A - 1)

由题目可以得知：

p 约等于 (B1!)%A1

A1是质数，由威尔逊定律可以得出：(A1 - 1)!%A1 = -1 % A

而B1 = A1 - randint(1e3,1e5)

(A1 - 1) * (A1 - 2) * (A1- 3) …… (B1+1) * B1！% A1 = -1 % A

推算一下：

(A1 - 2) * (A1- 3) …… (B1+1) * B1！% A1 = 1 % A1

(A1 - 2) * (A1- 3) …… (B1+1)与 B1！% A1是关于A1的模逆，这样就能求出B1！% A1的值了

然后通过在通过sympy.nextprime()函数算出p

import sympy
import math
import gmpy2
from Crypto.Util.number import *
A1 = 21856963452461630437348278434191434000066076750419027493852463513469865262064340836613831066602300959772632397773487317560339056658299954464169264467234407
B1 = 21856963452461630437348278434191434000066076750419027493852463513469865262064340836613831066602300959772632397773487317560339056658299954464169264467140596
A2 = 16466113115839228119767887899308820025749260933863446888224167169857612178664139545726340867406790754560227516013796269941438076818194617030304851858418927
B2 = 16466113115839228119767887899308820025749260933863446888224167169857612178664139545726340867406790754560227516013796269941438076818194617030304851858351026
n = 85492663786275292159831603391083876175149354309327673008716627650718160585639723100793347534649628330416631255660901307533909900431413447524262332232659153047067908693481947121069070451562822417357656432171870951184673132554213690123308042697361969986360375060954702920656364144154145812838558365334172935931441424096270206140691814662318562696925767991937369782627908408239087358033165410020690152067715711112732252038588432896758405898709010342467882264362733
c = 75700883021669577739329316795450706204502635802310731477156998834710820770245219468703245302009998932067080383977560299708060476222089630209972629755965140317526034680452483360917378812244365884527186056341888615564335560765053550155758362271622330017433403027261127561225585912484777829588501213961110690451987625502701331485141639684356427316905122995759825241133872734362716041819819948645662803292418802204430874521342108413623635150475963121220095236776428

def get_value(A,B):
	s = 1
	for i in range(B+1,A-1):
		s *= i
		s %= A
	value = gmpy2.invert(s,A)
	return sympy.nextprime(value)
p = get_value(A1,B1)
q = get_value(A2,B2)

r = n//p//q
phi = (p-1)*(q-1)*(r-1)
e=0x1001

d = gmpy2.invert(e,phi)
m = pow(c,d,n)
flag = long_to_bytes(m)
print(flag)
# RoarCTF{wm-CongrAtu1ation4-1t4-ju4t-A-bAby-R4A}

ke1os' blog

rsa合集

基础知识

数论知识

rsa加密算法

yafu的使用

中国剩余定理

例题：蓝桥杯2022年python B组试题B：寻找整数

各种题型

基础解法

rsarsa （基础解法）

RSAROOL (在线分解)

RSA (基础解法)

[ACTF新生赛2020]crypto-rsa0 (zip伪加密)

misc zip伪加密

[GUET-CTF2019]BabyRSA （z3）

[HDCTF2019]bbbbbbrsa (爆破e)

RSA (公钥解析1)

[AFCTF2018]可怜的RSA (公钥解析2 + PKCS1_OAEP)

模不互质

ezrsa

dp泄露

RSA2 (dp泄露)

共模攻击

RSA3 (共模攻击)

RSA & what (共模攻击+base64隐写)

已知dp、dq

RSA1 （已知dp、dq）

低加密指数攻击

dangerous RSA （低加密指数攻击）

公因数分解n

[BJDCTF2020]RSA（公因数分解n+爆破e）

RSA5（公因数求解）

低加密指数广播攻击(中国剩余定理)

RSA4 (中国剩余定理+低加密指数攻击)

rsa-wiener-attack

rsa2

方法一：在线分解

方法二：rsa-wiener-attack

数学推理

[BJDCTF2020]easyrsa （反三角函数求导）

[RoarCTF2019]RSA （推导+爆破e）

[RoarCTF2019]babyRSA (威尔逊定理)